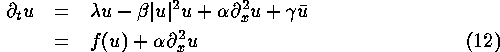
This theorem can be directly applied to the case of chaos-driven walk along a straight line, as recently described by Coullet and Emilsson [11]. This is Ising-Bloch wall dynamics in a modified Complex Ginzburg-Landau Equation:
for 
and 
.
At some parameter values, there are two stable equilibria 
in
the spatially homogeneous system 
, and solutions are
considered which asymptotically approach one equilibrium at
and the other at 
. This
equation is invariant under the group of translations along the x
axis. Reduction by this group, in the same style as we did it for
reaction-diffusion system (1) and Euclidean group 
, yields
the quotient system
for dynamic variables v and c, where
and 
could be chosen, say 
or
. X can be considered as the wall coordinate,
then drift along the group is the wall motion, and is described simply
by
Coullet and Emilsson [11] simulated the dynamics of the wall solutions and analyzed them in terms of the quantity M(t) defined as
which is invariant under the group, i.e. is a functional of the
quotient system (13). At some parameter values, they have
found that time-delay plots M(t) vs 
showed pictures
typical for chaotic attractors. Assuming that this implies invariant
measure, ergodicity and decaying correlation functions, we can apply
the Theorem, by identifying the semiflow generated by (13)
with 
of the Theorem, X with q and c with V. In
accordance with the statement of the Theorem, in the case of even
distribution of the velocity, which took place in a region of
parameters, Coullet and Emilsson observed `diffusive' motion with a
root mean squared displacement that scaled as 
. In the case
of non-even distribution which happened in between the `diffusive'
parameter range, the root mean squared displacement scaled as t,
which might correspond to the superposition of directed and Brownian
motion.
