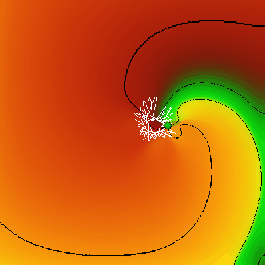
Spiral waves provide one of the most striking examples of pattern formation in nonlinear active media and have attracted attention since their description in the Belousov-Zhabotinsky (BZ) chemical reaction medium (Zaikin, 1970). They have been described in many other systems and models (Swinney & Krinsky, 1990; Holden et al. 1991), and in cardiac muscle they are of potentially vital interest, as they underly some lethal arhythmmias (Gray & Jalife 1996).
Figure 1: Spiral wave, isolines, tip and its trajectory, in a model of
ventricular tissue. Medium is colour-coded according to values of two
field components, an activation variable (transmembrane voltage, red
colour component intensity) and a recovery variable ( 
inactivation gate, green colour component intensity), details of the
model can be found in (Biktashev & Holden 1996). The wave irregularly
rotates counterclockwise. Black lines are the chosen isolines of the
two variables, the blue ball at their intersection is the tip of the
spiral wave. The white line shows the trajectory of the tip over last
few rotations. The rotation is approximately biperiodic, modulated by
some slow processes.
Spiral waves appear as rotating waves of chemical or other activity, that propagate through a stationary medium as a wave of synchronization of phase of self-oscillations or excitation, without any bulk movement of the medium. Typically they can be approximated by an Archimedean spiral, rotating with roughly constant speed. Soon after the discovery of spiral waves, Winfree (1973) examined in detail the dynamics of the tips of the spirals in the BZ reaction and found that these dynamics may not necessarily be steady, but that the spiral tip may describe complicated trajectories, which he called `meander'. An extensive computational, phenomenological study of meander patterns (Zykov 1986; Karma 1990; Barkley et al. 1990; Winfree 1991; Plesser& Müller 1995) has shown that they exhibit common features. Early computational work used simple, two-component FitzHugh-Nagumo-like models; however, essentially the same meander patterns have been observed in high order, detailed models of excitation propagation in heart muscle (Efimov et al. 1995; Biktashev & Holden 1996), where the particular type of meander relates to physiological properties of the tissue (Fig. 1).
Barkley et al. (1990) have studied numerically the change in type of
meander in a variant of the FitzHugh-Nagumo model, and found that the
transition from steady periodic rotation to the meander can exhibit
features typical for a supercritical Andronov-Hopf bifurcation, namely, a
linear decrease of the absolute value of the real part of the leading
eigenvalue as the bifurcation is approached and an 
-growth of deviation of the meander pattern from steady rotation
in the supercritical region. This led to the hypothesis that the
onset of meander is due to a secondary Hopf bifurcation from a periodic
motion (the steady rotation) to biperiodic one (the meander). A
detailed quantitative experimental study of tip trajectories in a
mathematical model of BZ reaction (Plesser & Müller 1995) has shown
that, with a good precision, tip meander can often be decomposed into
two periodic motions.
The question of possible resonances between the two periods arises naturally. Consideration of the 1:1 resonance led Barkley (1994) to propose a model form ODE system for this bifurcation. This model system was chosen to mimick both the bifurcation and the Euclidean symmetry by means of the simplest possible ODE system. Subsequent exploration of this system has led to the observation that no locking or entrainment between the two frequencies occur, which has proved to result from the symmetry built into the foundation of this system. Thus, it has become evident that the explanation of the phenomenon of spiral wave meander lies in the Euclidean symmetry of the plane on which they rotate. This is in agreement with general rigorous results by Rand (1982) within the context of rotating fluids in hydrodynamics and Renardy (1982) on bifurcations from rotating waves in abstract evolution equations possessing continuous symmetry groups.
In this paper, we apply ideas of the theory of dynamical systems with symmetry to the explanation of spiral wave meander. The abstract theoretical construct we use has a very clear ``physical interpretation'', which is to reduce the system with symmetry to a generic one, by moving to the frame of reference attached to the tip of the spiral. If the dynamics of the reduced system is ``coherent'', i.e. has a low dimensional attractor, then the motion of the tip can be described by an appropriate closed ODE system.
After this paper was submitted, we were informed of the related work of Fiedler (1995), Wulff (1996a, b) and Golubitsky et al. (1996).
