Critical Strip Explorer

This is a 2026 rebuild in JavaScript of the original Java applet Critical Strip Explorer (version 0.67), which was written by Raymond Manzoni based on my suggestions. Browsers stopped running Java applets around 2015–2017, so the original had been dead for roughly a decade; this version does the same job using the canvas element, and should keep working. The mathematics, the controls and the idea are all Raymond's and mine from the original — the code underneath is new. (If you are Raymond and you are reading this: hello, and thank you. Get in touch.)

There are two planes here, and they are different planes, which is why they get a frame each. On the left you choose s: move the pointer and the readout follows it, and click if you want to hold a value while you look at something else. On the right is the plane ζ takes its values in. The chain begins at the origin, each segment is one term of the series, so its vertices are the partial sums and its far end is ζ(s).

Each pane pans and zooms on its own, with the gestures you already use: a two-finger scroll moves the plane, a pinch (or ctrl and scroll) zooms about the pointer, a drag moves the right-hand pane, and a double-click puts a pane back where it started. The figure under each pane says how much of that plane you are looking at. Nothing about the left pane changes what the right one shows: they share a value of s and nothing else.

The reason to zoom the right-hand pane hard is the thing this whole application exists to show. Set s on the critical line and walk up it — by dragging in the left pane, or by pressing walk the critical line — and at a nontrivial zero the end of the chain arrives at the origin. Zoomed in far enough, you can watch it get there and leave again.

Constraining the value of x to be Re[s] = 1/2 will allow you to explore the behaviour of zeta on the critical line, and (in theory) to manually "find" nontrivial zeros on the critical line. As well as the x and y constraints, there are also the possibilities of constraining the phase and the modulus of s, in order to explore the behaviour of zeta along rays and around circles centred at the origin.

The vertices of the polygonal line which you see correspond to the partial sums (or products) in an infinite sum (or product) expression for the zeta function. There are a number of options in the expression menu:

• Finite zeta sum is the most familiar expression for zeta(s), converging for Re[s] > 1. Obviously we can only approximate the infinite sum with a finite number of terms. This is the case for all options, but you are free to choose the number of terms ("number of points").
   
• Mirror zeta sum combines the functional equation with the usual sum to produce an expression which converges for Re[s] < 0.
   
• Alternate zeta sum makes use of a well-known technique for extending the usual sum into the critical strip (i.e. values of zeta(s) where Re[s] > 0) involving a sum whose terms have alternating signs: \[\sum_{n=1}^{\infty}(-1)^{n}n^{-s}\;+\;\sum_{n=1}^{\infty}n^{-s}\;=\;2\sum_{n=2,4,\ldots}n^{-s}\] \[\sum_{n=1}^{\infty}(-1)^{n}n^{-s}\;+\;\zeta(s)\;=\;2^{1-s}\zeta(s).\] \[\zeta(s)\;=\;\frac{1}{1-2^{1-s}}\sum_{n=1}^{\infty}(-1)^{n-1}n^{-s}\]
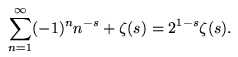
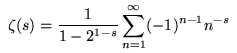
• Mirror alternate sum combines the functional equation with the "alternate zeta sum" in order to produce an expression which converges when Re[s] < 1.
   
• Finite Euler product is based on the usual product-over-primes form of zeta, also convergent when Re[s] > 1.
   

Hence, with each of these options, the polygonal line "spirals in" on the value of the zeta function at the selected s = x + iy.

The higher up the critical strip you go, the stranger the chain becomes on its way to the same place. It is worth zooming out to watch.

A note on accuracy. The polygonal line shows the raw partial sums, exactly as the original did — nothing is accelerated or smoothed. That means convergence on the critical line is genuinely slow: the alternating series converges like N^−1/2 there, so even 20,000 terms leaves an error of order 10⁻³. That slowness is not a defect of the display, it is the phenomenon — it is why the spiral keeps circling instead of settling, and why finding a zero by eye is hard. Convergence acceleration would give you a more accurate number and a far less honest picture.

Glen Pugh has produced a couple of related applets: a "Dirichlet Series Animation" depicting "wandering partial sums" and one which plots the behaviour of zeta along the critical line. Jan van Delden has produced another applet based on Pugh's.