
the "encoding" of the distribution of prime numbers by the nontrivial
zeros of the Riemann zeta function [common approach]
The distribution
of prime numbers is most simply expressed as the (discontinuous) step
function 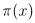 , where
, where
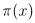 is the number of primes less than or equal to x.
is the number of primes less than or equal to x.

It turns out that 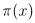 can be expressed
exactly as the limit of a sequence of smooth functions Rn
(x). To define Rn(x) we first
introduce the
logarithmic integral function Li(x), which appears throughout the
analytical theory of the prime distribution:
can be expressed
exactly as the limit of a sequence of smooth functions Rn
(x). To define Rn(x) we first
introduce the
logarithmic integral function Li(x), which appears throughout the
analytical theory of the prime distribution:

This is a smooth function which simply gives the area under the curve of the function 1/log u in the interval [2,x].
Don Zagier explains the reasoning behind the function Li in his excellent introductory article "The first 50 million prime numbers" (from The Mathematical Intelligencer 0 (1977) 7-19, based on his inaugural lecture held at Bonn University, May 5, 1975):
"[A] good approximation to, which was first given by Gauss is obtained by taking as starting point the empirical fact that the frequency of prime numbers near a very large number x is almost exactly 1/log x. From this, the number of prime numbers up to x should be approximately given by the logarithmic sum
Ls(x) = 1/log 2 + 1/log 3 + ... + 1/log x
or, what is essentially the same, by the logarithmic integral
Using Li(x) we then define another smooth function, R(x), first introduced by Riemann in his original eight-page paper, and given by
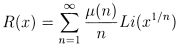
 are
Möbius
Numbers. Certain useful comments and
graphs relating to this function appear in
Riesel's book.
are
Möbius
Numbers. Certain useful comments and
graphs relating to this function appear in
Riesel's book.
In the aforementioned article, Don Zagier goes on to explain the reasoning behind the Riemann function:
"There is one more approximation which I would like to mention. Riemann's research on prime numbers suggests that the probability for a large number x to be prime should be even closer to 1/log x if one counted not only the prime numbers but also the powers of primes, counting the square of a prime as half a prime, the cube of a prime as a third, etc. This leads to the approximation:

or, equivalently [by means of the Möbius inversion formula]

[Note that the minus signs result from Möbius numbers and do not continue indefinitely]The function on the right side of this formula is denoted by R(x), in honour of Riemann. It represents an amazingly good approximation to
...
For those in the audience who know a little function theory, perhaps I might add that R(x) is an entire function of log x, given by the rapidly converging power series:where
is the Riemann zeta function."

Here we see the zeros of the Riemann zeta function in the complex plane. These fall into two categories, trivial and nontrivial zeros.
Here are some tables on nontrivial zeros compliled by Andrew Odlyzko.
The trivial zeros are simply the negative even integers. The nontrivial zeros are known to all lie in the critical strip 0 < Re[s] < 1, and always come in complex conjugate pairs. All known nontrivial zeros lie on the critical line Re[s] = 1/2. The Riemann Hypothesis states that they all lie on this line.
The difference between the prime counting function
and its "amazingly good approximation"
R(x), i.e. the fluctuations in the distribution of
primes, can be expressed in terms of the entire set
of zeros of zeta, which we shall represent by  ,
via the function R itself:
,
via the function R itself:

 are complex values, so here R is the
analytic continuation of the real-valued function R defined previously.
This was mentioned above by Zagier, and is known as
the Gram Series
expansion:
are complex values, so here R is the
analytic continuation of the real-valued function R defined previously.
This was mentioned above by Zagier, and is known as
the Gram Series
expansion:

 separates into two sums,
over the trivial and nontrivial zeros, respectively. The former sum
is of course just R(x-2) + R(x-4) +
R(x-6) + ..., and the latter can be written
separates into two sums,
over the trivial and nontrivial zeros, respectively. The former sum
is of course just R(x-2) + R(x-4) +
R(x-6) + ..., and the latter can be written
![$\sum_{k=1}^{\infty}[R(x^{\rho_{k}})+R(x^{\rho_{-k}})]$](nontrivsum.jpg)
 and
and
 cancel each others' imaginary parts, so
cancel each others' imaginary parts, so
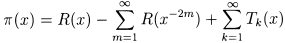
where the

are real-valued.
We can now define the sequence of functions Rn(x)
which approximate 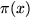 in limit:
in limit:

An excellent illustration of this is provided on page
55 of Hans Riesel's book, which compares
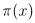 with
with

Below we see an animated image, each successive frame being the result of adding another Tn(x) to the function

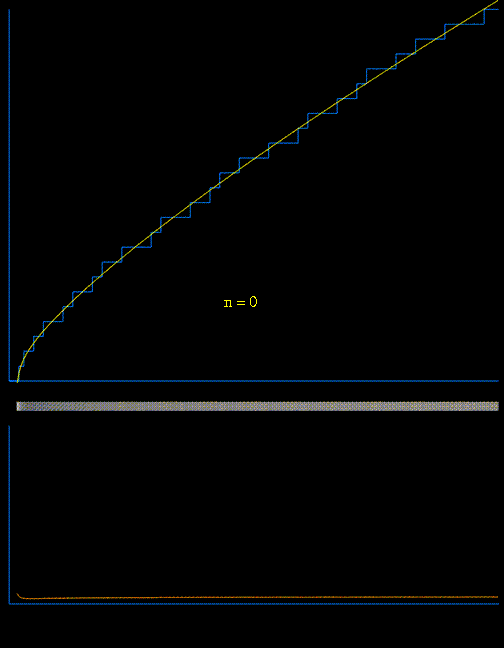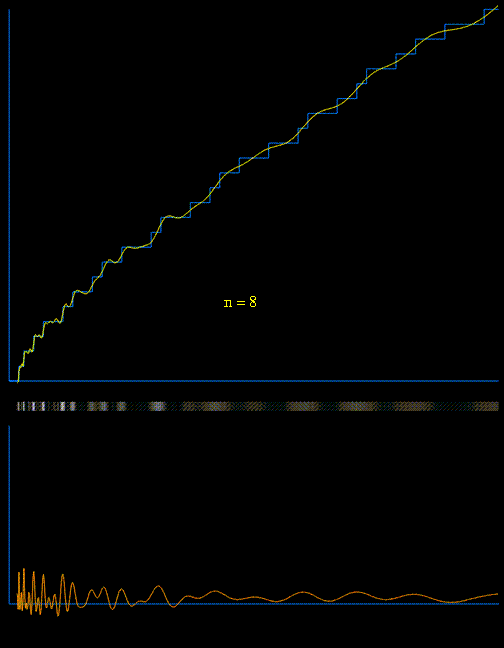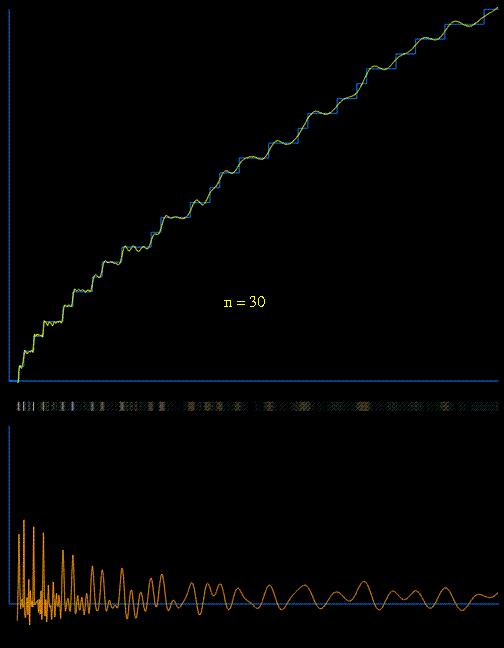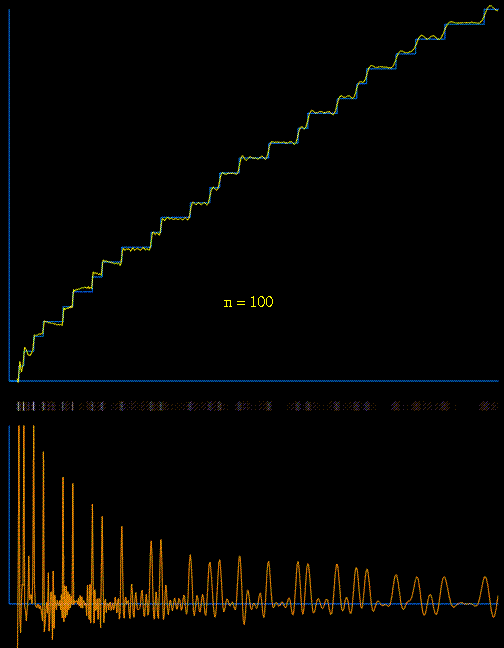
[animation courtesy of Raymond Manzoni]
The lower animated graph is the derivative of the function above, and we see the positions of the primes emerging as Dirac delta-type spikes. The horizontal bar in the middle has been constructed so that the intensity of brightness is related to the absolute value of the derivative. In this way we see the positions of the primes gradually emerge as narrow bands of light.
To summarise: R(x) is asymptotic to
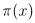 , and is a particularly good estimate for the
distribution of primes. It is a refinement of Li(x), itself a
refinement of the basic
, and is a particularly good estimate for the
distribution of primes. It is a refinement of Li(x), itself a
refinement of the basic  given by the
prime number theorem. R can be thought of as describing the "average"
behaviour of the primes.
The correction terms Tk(x), which are defined using
the zeros of the zeta function collectively describe the
local fluctuations.
given by the
prime number theorem. R can be thought of as describing the "average"
behaviour of the primes.
The correction terms Tk(x), which are defined using
the zeros of the zeta function collectively describe the
local fluctuations.
It is quite remarkable that a single smooth function can provide not only an
excellent estimate for 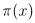 , but also, through
an infinite sum of (complex) exponential "rescalings", an exact expression for
the fluctuations
, but also, through
an infinite sum of (complex) exponential "rescalings", an exact expression for
the fluctuations
 .
.
In other words, with the single function R and the set of nontrivial zeta
zeros, we can exactly reconstruct the prime counting function 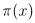 . Consequently, the sequence of nontrivial
zeta zeros is sometimes described as being "dual" to the sequence of primes.
. Consequently, the sequence of nontrivial
zeta zeros is sometimes described as being "dual" to the sequence of primes.
further items of interest
"We will...write

...Nothing is known about the  , but they are thought likely to be transcendental numbers, algebraically independent of any reasonable numbers that have ever been considered."
, but they are thought likely to be transcendental numbers, algebraically independent of any reasonable numbers that have ever been considered."
A.M. Odlyzko on the nontrivial zeros of the zeta function, from "Primes, Quantum Chaos, and Computers"
"What Riemann observed (and Hadamard later proved) was that the zeta function can also be written as a product over its zeroes in the complex plane:

where  ,
,
 , etc. are the complex
numbers for which
, etc. are the complex
numbers for which  ,
and f(s) is
a fairly simple "fudge factor". Riemann showed that by equating the
logarithms of these two expressions for the zeta function it's possible
to derive...a whole sequence of increasingly accurate approximations -
in effect, an exact formula for
,
and f(s) is
a fairly simple "fudge factor". Riemann showed that by equating the
logarithms of these two expressions for the zeta function it's possible
to derive...a whole sequence of increasingly accurate approximations -
in effect, an exact formula for
 ."
."
Barry Cipra, from "A Prime Case of Chaos" (1999)
"One of Riemann's great achievements [1,2] was to give an exact formula for
 , constructed as follow. First,
, constructed as follow. First,
 is expressed in terms of a function J(x) [1, Chapter 1] that has jumps at prime powers:
is expressed in terms of a function J(x) [1, Chapter 1] that has jumps at prime powers:

In this formula,  are the Möbius numbers (1, –1, –1, 0, –1, 1, ...). Each of the
partial densities J ' is the sum of a smooth part and an infinite series of oscillations:
are the Möbius numbers (1, –1, –1, 0, –1, 1, ...). Each of the
partial densities J ' is the sum of a smooth part and an infinite series of oscillations:

(see section 1.18 of [1]). Here the numbers tn in the
oscillatory contributions are related to the complex Riemann zeros...It is
known that the complex zeros (i.e., those with nonzero imaginary part) of
 lie in the "critical strip" (Re(s)
between 0 and 1) , and the Riemann hypothesis states that in fact all
these zeros lie on the "critical line" Re(s) = 1/2. The numbers
tn are defined by
lie in the "critical strip" (Re(s)
between 0 and 1) , and the Riemann hypothesis states that in fact all
these zeros lie on the "critical line" Re(s) = 1/2. The numbers
tn are defined by
![$\zeta(\frac{1}{2}+it_{n})=0\;\;(Re[t_{n}]\neq0$](zetavanishing.jpg)
If the Riemann hypothesis is true, all the (infinitely many) tn are real, and are the heights of the zeros above the real s axis. It is known by computation that 1,500,000,001 complex zeros lie on the line [3]."
M.V. Berry and J.P. Keating, "The Riemann Zeros and Eigenvalue Asymptotics", SIAM Review 41, no. 2, page 237.
"...there is an explicit formula for the density of states of the zeros...that is directly analogous to the Gutzwiller trace formula for a completely chaotic system:

where the first sum includes all primes p, and the mean density of states is given by

or using Stirling's formula, as E tends to infinity, by
 ."
."
E.B. Bogomolny and J.P. Keating, "Random matrix theory and the Riemann zeros I: three- and four-point correlations", Nonlinearity 8 (1995) 1115–1131
[1] H.M. Edwards, Riemann's Zeta Function, Academic Press, New York, London, 1974.
[2] D. Zagier, "The first 50 million prime numbers", Mathematical Intelligencer 0 (1977), 7–19.
[3] J. Van de Lune, H.J.J. te Riele, and D.T. Winter, "On the zeros of the Riemann zeta function in the critical strip. IV", Math. Comp. 46 (1986), 667–681.
the more elegant approach
number theory and physics archive prime numbers: FAQ and resources
mystery new search home