M.L. Lapidus, "The sound of fractal strings and the Riemann Hypothesis" (preprint 05/2015)

"We give an overview of the intimate connections between natural direct and inverse spectral problems for fractal strings, on the one hand, and the Riemann zeta function and the Riemann hypothesis, on the other hand (in joint works of the author with Carl Pomerance and Helmut Maier, respectively). We also briefly discuss closely related developments, including the theory of (fractal) complex dimensions (by the author and many of his collaborators, including especially Machiel van Frankenhuijsen), quantized number theory and the spectral operator (jointly with Hafedh Herichi), and some other works of the author (and several of his collaborators)."
 

M.L. Lapidus, In Search of the Riemann Zeros (AMS, 2008)
 

M.L. Lapidus and M. van Frankenhuysen, Fractal Geometry and Number Theory: Fractal Strings and Zeros of Zeta Functions(Birkhauser, 2000)
 

M.L. Lapidus and C. He, Generalized Minkowski Content, Spectrum of Fractal Drums, Fractal Strings and the Riemann-Zeta-Function (AMS, 1997)

"Studies the effect of nonpower-like irregularities of the geometry of the fractal boundary on the spectrum of fractal drums and especially of fractal strings. The authors use the notion of generalized Minkowski content, which is defined through some suitable gauge functions other than the power functions. By so doing, they obtain more precise estimates in the situation in which the power function is not the natural gauge function."
 

M.L. Lapidus and M. van Frankenhuysen, eds., Dynamical, Spectral, and Arithmetic Zeta-Functions, Contemporary Mathematics volume 290 (AMS, 2001)

"This volume grew out of the special session on dynamical, spectral, and arithmetic zeta functions held at the annual meeting of the American Mathematical Society in San Antonio, but also includes four articles that were invited to be part of the collection. The purpose of the meeting was to bring together leading researchers, to find links and analogies between their fields, and to explore new methods. The papers discuss dynamical systems, spectral geometry on hyperbolic manifolds, trace formulas in geometry and in arithmetic, as well as computational work on the Riemann zeta function."
 

M.L. Lapidus and C. Pomerance, "Fonction zeta de Riemann et conjecture de Weyl-Berry pour les tambours fractals", C. R. Acad. Sci. Paris Ser. I Math. 310 (1990) 343-348.

M.L. Lapidus and H. Maier, "Hypothese de Riemann, cordes fractales vibrantes et conjecture de Weyl-Berry modifiee", C. R. Acad. Sci Paris Ser. I Math. 313 (1991) 19-24.

"Jointly with C. Pomerance, the first author has recently proved in dimension one the "modified Weyl-Berry conjecture" formulated in his earlier work on the vibrations of fractal drums. Here, we show, in particular, that (still in dimension one) the converse of this conjecture is not true in the "midfractal" case and that it is true everywhere else if and only if the Riemann hypothesis is true. We thus obrain a new characterization of the Riemann hypothesis by means of a inverse spectral problem."
 

M.L. Lapidus, "Spectral and fractal geometry: From the Weyl-Berry conjecture for the vibrations of fractal drums to the Riemann zeta-function" (from Ordinary and Partial Differential Equations and Mathematical Physics, Ed. C. Bennewitz - Proceedings of the Fourth UAB International Conference, Birmingham 1990) (Academic Press, 1992) 151-182.

M.L. Lapidus, "Vibrations of fractal drums, the Riemann hypothesis, waves in fractal media, and the Weyl-Berry conjecture" (from Ordinary and Partial Differential Equations, Eds. B. Sleeman, et. al. - volume IV, Proceedings of the Twelfth International Conference, Dundee 1992) (Pitman Research Notes in Mathematics Series 289, Longman Scientific and Technical, 1993) 126-209.

M.L. Lapidus and C. Pomerance, "The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums", Proceedings of the London Mathematical Society (3) 66 (1993) 41-69.

"Based on his earlier work on the vibrations of 'drums with fractal boundary', the first author has refined M.V. Berry's conjecture that extended from the 'smooth' to the 'fractal' case H. Weyl's conjecture for the asymptotics of the eigenvalues of the Laplacian on a bounded open subset of Rⁿ. We solve here in the one-dimensional case (that is n = 1) this 'modified Weyl-Berry conjecture'. We discover, in the process, some unexpected and intriguing connections between spectral geometry, fractal geometry and the Riemann zeta-function. we therefore show that one can 'hear' (tha is, recover from the spectrum) not only Minkowski fractal dimension of the boundary - as was established previously by the first author - but also, under the stronger assumptions of the conjecture, its Minkowski content (a 'fractal' analogue of its 'length').

We also prove (still in dimension one) a related conjecture of the first author, as well as its converse, which characterizes the situation when the error estimates of the aforementioned paper are sharp."
 

M.L. Lapidus and H. Maier, "The Riemann Hypothesis and inverse spectral problems for fractal strings", Journal of the London Mathematical Society (second edition) 52 (1995) 15-34.

"Motivated in part by the first author's work on the Weyl-Berry conjecture for the vibrations of 'fractal drums' (that is, 'drums with fractal boundary'), M.L. Lapidus and C. Pomerance have studied a direct spectral problem for the vibrations of 'fractal strings' (that is, one-dimensional 'fractal drums') and establihed in the process some unexpected connections with the Riemann zeta-function 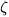= in the 'critical interval' 0 < s < 1. In this paper we show, in particular, that the converse of their theorem (suitably interpreted as a natural inverse spectral problem for fractal strings, with boundary of Minkowski fractal dimension D in (0,1)) is not true in the 'midfractal' case when D = 1/2, but that it is true for all other D in the critical interval (0,1) if and only if the Riemann hypothesis is true. We thus obtain a new characterization of the Riemann hypothesis by means of an inverse spectral problem. (Actually, we prove the following stronger result: for a given D in (0,1), the above inverse spectral problem is equivalent to the 'partial Riemann hypothesis' for D, according to which 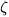= does not have any zero on the vertical line Re s = D.) Therefore, in some very precise sense, our work shows that the question (a la Marc Kac) "Can one hear the shape of a fractal string?" - now interpreted as a suitable converse (namely, the above inverse problem) - is intimately connected with the existence of zeros of 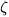= in the critical strip 0 < Re s < 1, and hence to the Riemann hypothesis."
 

M.L. Lapidus and C. Pomerance, "Counterexamples to the modified Weyl-Berry conjecture on fractal drums", Mathematical Proceedings of the Cambridge Philosophical Society 119 (1996) 167-178.

C. He and M.L. Lapidus, "Generalized Minkowski content, spectrum of fractal drums and strings", Mathematical Research Letters 3 (1996) 31-40.

"In [La1], the second author has obtained a sharp error estimate for the eigenvalue distribution of the Laplacian on bounded open sets \Omega \sub Rⁿ with fractal boundaries (i.e., 'fractal drums'). Further, he and Pomerance studied in detail the case of 'fractal strings' (i.e., n = 1) and established in the process some unexpected connections with the Riemann zeta-functions 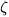= in the 'critical strip' 0 < Re s <1. Later on, still when n = 1, Lapidus and Maier obtained a new characterization of the Riemann hypothesis by means of an associated inverse spectral problem.

In this paper, we will extend most of these results by using, in particular, the notion of generalized Minkowski content which is defined through some suitable 'gauge functions' other than the power functions. In this situation when the power function is not the natural 'gauge function', this will enable us to obtain more precise estimates, with a broader potential range of applications than in the above papers."
 

M.L. Lapidus and M. van Frankenhuysen, "Complex dimensions of fractal strings and oscillatory phenomena" and "Zeta-functions and explicit formulas for the geometry and spectrum of fractal strings", Abstracts 918-35-537 and 918-35-539, Abstracts Amer. Math. Soc. 18, no.1 (1997) 82-83.

M.L. Lapidus and M. van Frankenhuysen, "Complex dimensions of fractal strings and explicit formulas for geometric and spectral zeta-functions", Preprint IHES/M/97/34, Institut des Hautes Etudes Scientifiques, Bures-sur-Yvette, France, April 1997.

M.L. Lapidus and M. van Frankenhuysen, "Complex dimensions and oscillatory phenomena, with applications to the geometry of fractal strings and to the critical zeros of zeta-functions", Preprint, IHES/M/97/38, Institut des Hautes Etudes Scientifiques, Bures-sur-Yvette, France, May 1997.

M.L. Lapidus and M. van Frankenhusen, "Complex dimensions of fractal strings and oscillatory phenomena in fractal geometry and arithmetic", from Spectral Problems in Geometry and Arithmetic (T. Branson,ed.), Contemporary Mathematics, vol. 237 (AMS, 1999) 87-105.

"We put the theory of Dirichlet series and integrals in the geometric setting of 'fractal strings' (one-dimensional drums with fractal boundary). The poles of a Dirichlet series thus acquire the geometric meaning of 'complex dimensions' of the associated fractal string, and they describe the geometric and spectral oscillations of this string by means of an 'explicit formula'. We define the 'spectral operator', which allows us to characterize the presence of critical zeros of zeta-functions from a large class of Dirichlet series as the questions of invertibility of this operator. We thus obtain a geometric reformulation of the generalized Riemann Hypothesis, thereby extending the earlier work of the first author with H. Maier. By considering the restriction of this operator to the subclass of 'generalized Cantor strings', we prove that zeta-functions from a large subclass of this class have no infinite sequence of zeros forming a vertical arithmetic progression. (For the special case of the Riemann zeta-function, this is Putnam's theorem.)

We make an extensive study of the complex dimensions of 'self-similar' fractal strings, to gain further insight into the kind of geometric infromation contained in the complex dimensions. We also obtain a formula for the volume of the tubular neighborhoods of a fractal string and draw an analogy with Riemannian geometry. Our work suggests to define 'fractality' as the presence of nonreal complex dimensions with positive real part."
 

M.L. Lapidus and M. van Frankenhuysen, "A prime orbit theorem for self-similar flows and Diophantine approximation", Contemporary Mathematics volume 290 (AMS 2001) 113-138.

[abstract:] "Assuming some regularity of the dynamical zeta function, we establish an explicit formula with an error term for the prime orbit counting function of a suspended flow. We define the subclass of self-similar flows, for which we give an extensive analysis of the error term in the corresponding prime orbit theorem."

M.L. Lapidus and M. van Frankenhuysen, "Complex dimensions of self-similar fractal strings and Diophantine approximation", to appear in Journal of Experimental Mathematics

[abstract:] "We study the solutions in s of a 'Dirichlet polynomial equation' m₁r₁^s + ^... + m_Mr_M^s = 1. We distinguish two cases. In the lattice case, when r_j = r^k_j are powers of a common base r, the equation corresponds to a polynomial equation, which is readily solved numerically by using a computer. In the nonlattice case, when some ratio log r_j/log r₁, j > 2, is irrational, we obtain information by approximating the equation by lattice equations of higher and higher degree. We show that the set of lattice equations is dense in the set of all equations, and deduce that the roots of a nonlattice Dirichlet polynomial equation have a quasiperiodic structure, which we study in detail both theoretically and numerically.

This question is connected with the study of the complex dimensions of self-siilar strings. Our results suggest, in particular, that a nonlattice string possesses a set of complex dimensions with countabley many real parts (fractal dimensions) which are dense in a connected interval. Morevover, we find dimension free regions of nonlattice self-similar strings. We illustrate our theory by means of several examples. In the long term, this work is aimed in part at developing a Diophantine approximation theory of (higher-dimensional) self-similar fractals, both qualitatively and quantitatively."
 

M.L. Lapidus and M. van Frankenhuijsen, "Fractality, self-similarity and complex dimensions", to appear in Proceedings of Symposia of Pure Mathematics, title: "Fractal Geometry and Applications: A Jubilee of Benoit Mandelbrot"

[abstract:] "We present an overview of a theory of complex dimensions of self-similar fractal strings, and compare this theory to the theory of varieties over a finite field from the geometric and the dynamical point of view. Then we combine the several strands to discuss a possible approach to establishing a cohomological interpretation of the complex dimensions."
 

T.W. Hilberdink and M.L. Lapidus, "Beurling zeta functions, generalised primes, and fractal membranes" (preprint 02/04)

Here is an excerpt from the introductory section:

B.M. Hambly and M.L. Lapidus, "Random fractal strings: their zeta functions, complex dimensions and spectral asymptotics" (preprint 02/04)

[abstract:] "In this paper a string is a sequence of positive non-increasing real numbers which sums to one. For our purposes a fractal string is a string formed from the lengths of removed sub-intervals created by a recursive decomposition of the unit interval. By using the so called complex dimensions of the string, the poles of an associated zeta function, it is possible to obtain detailed information about the behaviour of the asymptotic properties of the string. We consider random versions of fractal strings. We show that using a random recursive self-similar construction it is possible to obtain similar results to those for deterministic self-similar strings. In the case of strings generated by the excursions of stable subordinators, we show that the complex dimensions can only lie on the real line. The results allow us to discuss the geometric and spectral asymptotics of one-dimensional domains with random fractal boundary."

H. Herichi and M.L. Lapidus, "Riemann zeroes and phase transitions via the spectral operator on fractal strings" (preprint 03/2012)

[abstract:] "The spectral operator was introduced by M. L. Lapidus and M. van Frankenhuijsen [La-vF3] in their reinterpretation of the earlier work of M. L. Lapidus and H. Maier [LaMa2] on inverse spectral problems and the Riemann hypothesis. In essence, it is a map that sends the geometry of a fractal string onto its spectrum. In this survey paper, we present the rigorous functional analytic framework given by the authors in [HerLa1] and within which to study the spectral operator. Furthermore, we also give a necessary and sufficient condition for the invertibility of the spectral operator (in the critical strip) and therefore obtain a new spectral and operator-theoretic reformulation of the Riemann hypothesis. More specifically, we show that the spectral operator is invertible (or equivalently, that zero does not belong to its spectrum) if and only if the Riemann zeta function $\zeta(s)$ does not have any zeroes on the vertical line $\Re(s)=c$. Hence, it is not invertible in the mid-fractal case when $c=1/2$, and it is invertible everywhere else (i.e., for all $c\in (0,1)$ with $c$ not equal to $1/2$ if and only if the Riemann hypothesis is true. We also show the existence of four types of (mathematical) phase transitions occurring for the spectral operator at the critical fractal dimension $c=1/2$ and $c=1$ concerning the shape of the spectrum, its boundedness, its invertibility as well as its quasi-invertibility."

M. Lapidus, "Towards quantized number theory: Spectral operators and an asymmetric criterion for the Riemann Hypothesis" (preprint 01/2015)

[abstract:] "Given $c \geq 0$, the spectral operator $\mathfrak{a} = \mathfrak{a}_c$ can be thought of intuitively as the operator which sends the geometry onto the spectrum of a fractal string of dimension not exceeding $c$. Rigorously, it turns out to coincide with a suitable quantization of the Riemann zeta function $\zeta = \zeta(s): \mathfrak{a} = \zeta (\partial)$, where $\partial = \partial_c$ is the infinitesimal shift of the real line acting on the weighted Hilbert space $L^2(\mathbb{R}, e^{-2ct} dt)$. In this paper, we establish a new asymmetric criterion for the Riemann hypothesis, expressed in terms of the invertibility of the spectral operator for all values of the dimension parameter $c \in (0, 1/2)$ (i.e., for all $c$ in the left half of the critical interval $(0,1)$). This corresponds (conditionally) to a mathematical (and perhaps also, physical) "phase transition" occurring in the midfractal case when $c = 1/2$. Both the universality and the non-universality of $\zeta = \zeta (s)$ in the right (resp., left) critical strip $\{1/2 < Re(s) < 1 \}$ (resp., $\{0 < Re(s) < 1/2 \}$) play a key role in this context. We also discuss earlier, related work of the author with H. Maier and with H. Herichi, respectively, in which were established symmetric criteria for the Riemann hypothesis, expressed respectively in terms of a family of natural inverse spectral problems for fractal strings of Minkowski dimension $D \in (0,1)$, with $D \neq 1/2$, and of the quasi-invertibility of the family of spectral operators $\mathfrak{a}_c$ (with $c \in (0,1)$, $c \neq 1/2$)."