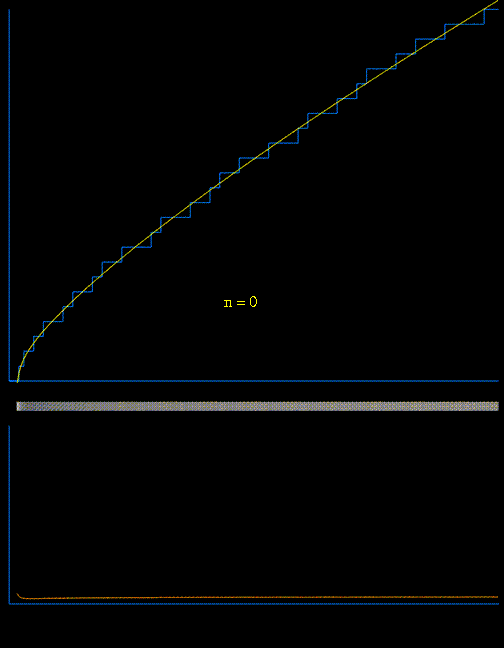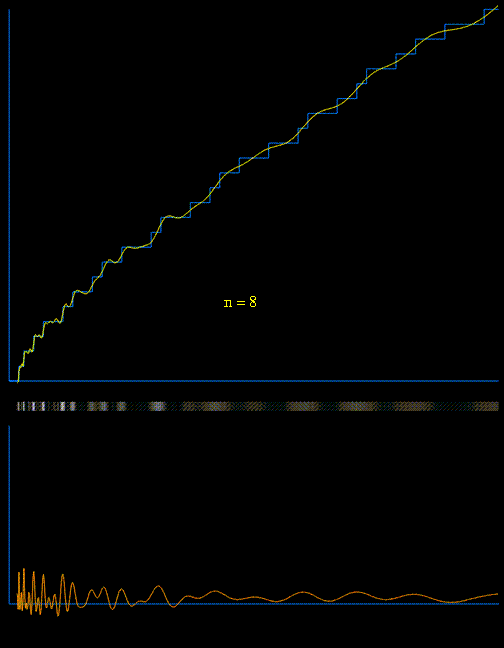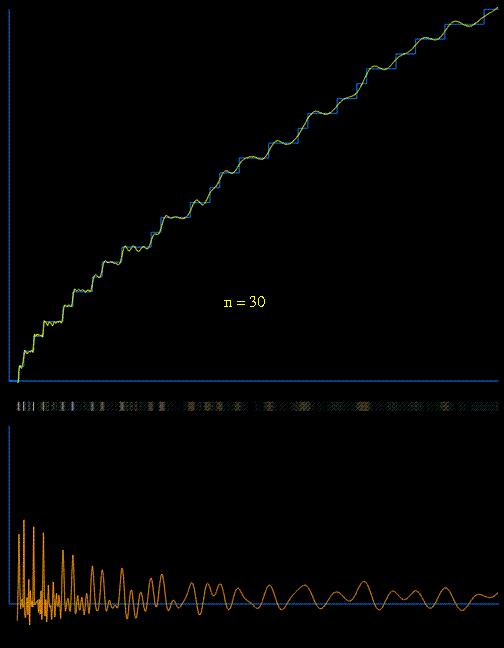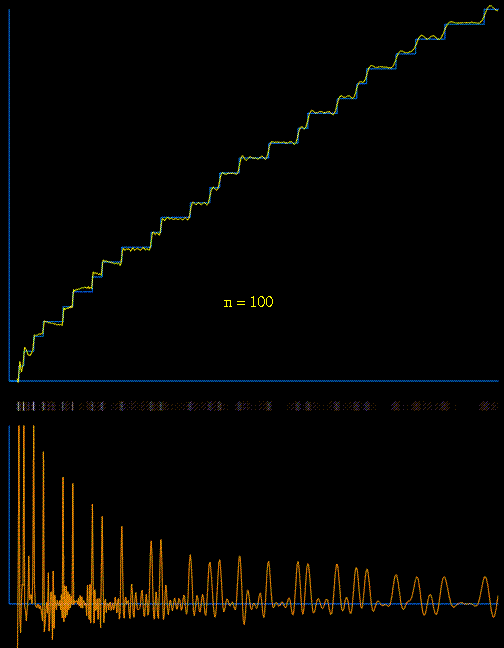
The approximation of the prime counting function
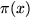(shown in blue) using the first 100 pairs of nontrivial zeros
, 
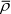of the Riemann zeta function in a variant of
von Mangoldt's explicit formula:
At each step, the current function (shown in yellow) is modified by adding a waveform whose frequency and amplitude are related to the next pair of nontrivial (complex) zeros in a simple and direct way.
The lower animated graph is the derivative of the function above, and we see the positions of the primes emerging as Dirac delta-type spikes. The horizontal bar in the middle has been constructed so that the intensity of brightness is related to the absolute value of the derivative. In this way we see the positions of the primes gradually emerge as narrow bands of light. Also available is a similar animation depicting the emergence of Chebyshev's function
, a logarithmically-weighted
prime counting function of great importance (for example in
the proof of the prime number theorem.)
archive tutorial mystery new search home contact