Filtering and smoothing

It is often useful to either low-pass filter (smooth) time series in order to reveal low-frequency features and trends, or to high-pass filter (detrend) time series in order to isolate high frequency transients (e.g. storms).

Some of the most commonly used filters are:

• Moving average MA(q)
  This simple class of low-pass filters is obtained by applying a running mean of length $q$ to the original series

  
  

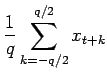  $$y_t = \frac{1}{q}\sum_{k=-q/2}^{q/2} x_{t+k}$$ (9.1)

  
  

  For example, the three month running mean filter MA(3) is useful for crudely filtering out intraseasonal oscillations. Note, however, that the sharp edges in the weights of this filter can causing spurious ringing (oscillation) and leakage into the smoothed output.

• Binomial filters $(1/2,1/2)^m$
  

  These smoother low-pass filters are obtained by repeatedly applying the MA(2) filter that has weights $(1/2,1/2)$. For example, with $m=4$ applications the binomial filter weights are given by $(1/2,1/2)^4=(1,4,6,4,1)/16$ which tail off smoothly towards zero near the edges. After many applications, the weights become Gaussian and the filtering approximates Gaussian kernel smoothing.

• Holt exponential smoother
  

  This simple and widely used recursive filter is obtained by iterating
  

  $$y_t = \alpha x_t+(1-\alpha)y_{t-1}$$ (9.2)

  
  where $\alpha<1$ is a tunable smoothing parameter. This low-pass filter gives most weight to most recent historical values and so provides the basis for a sensible forecasting procedure when applied to trend, seasonal, and irregular components (Holt-Winters forecasting).

• Detrending (high-pass) filters
  

  High-pass filtering can most easily be performed by subtracting a suitably low-pass filtered series from the original series. The detrended residuals $x_t-y_t$ contain the high-pass component of $x$. For example, the backward difference detrending filter $\Delta x = x_t-x_{t-1}$ is simply twice the residual obtained by removing a MA(2) low-pass filtered trend from a time series. It is very efficient at removing stochastic trends and is often used to detrend non-stationary time series (e.g. random walks in commodity prices).

  Figure: Time series plot of one-year backward differences in monthly mean sea-level pressure at Darwin from the period January 1951 to July 2000. The differencing has efficiently removed both the seasonal component and the long-term trend thereby revealing short-term interannual variations.