



Next: Example 2: Exponential distribution
Up: Theoretical continuous distributions
Previous: Theoretical continuous distributions
Contents
A random variable is uniformly distributed
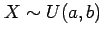 when
when
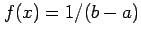 for
for
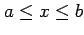 and zero otherwise.
In other words, the random variable is equally likely to
take any value in the interval
and zero otherwise.
In other words, the random variable is equally likely to
take any value in the interval ![$ [a,b]$](img228.png) .
Standard (pseudo)random number generators on computers and
pocket calculators generate random numbers from 0 to 1 that
are distributed as
.
Standard (pseudo)random number generators on computers and
pocket calculators generate random numbers from 0 to 1 that
are distributed as
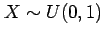 .
.
David Stephenson
2005-09-30