



Next: Example 1: Uniform distribution
Up: Distributions of continuous variables
Previous: Empirical estimates
Contents
Because the estimates are based on a finite number of
sample values, the empirical (cumulative) distribution function (e.d.f.)
goes up in small discrete steps rather than being a truly
smooth function defined for all values.
To obtain a continuous differentiable estimate of the c.d.f.,
the probability distribution can be smoothed using either
moving average filters or smoothing splines or kernels.
This is known as a non parametric approach since it does
not depend on estimating any set of parameters.
An alternative approach is to approximate
the empirical distribution function by using
an appropriate class of smooth analytic function.
For a particular class of function (probability model),
the location, spread, and/or shape of the probability density function
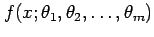 is controlled by
the values of a small number of population parameters
is controlled by
the values of a small number of population parameters
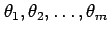 .
This is known as a parametric approach since it
depends on estimating a set of parameters.
.
This is known as a parametric approach since it
depends on estimating a set of parameters.
The following sections will describe briefly some (but not all)
of the most commonly used theoretical probability distributions.
Figure:
Examples of continuous probability density functions:
(a) Uniform with  and
and  ,
(b) Normal with
,
(b) Normal with 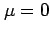 and
and 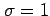 ,
and
(c) Gamma with
,
and
(c) Gamma with 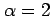 and
and 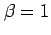 .
.
|
Subsections




Next: Example 1: Uniform distribution
Up: Distributions of continuous variables
Previous: Empirical estimates
Contents
David Stephenson
2005-09-30
![]() is controlled by
the values of a small number of population parameters
is controlled by
the values of a small number of population parameters
![]() .
This is known as a parametric approach since it
depends on estimating a set of parameters.
.
This is known as a parametric approach since it
depends on estimating a set of parameters.