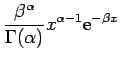 |
(4.8) |
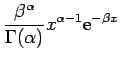 |
(4.8) |
The gamma distribution is useful for describing positively skewed
positive variables such as rainfall totals.
A nice additive property of gamma distributed variables is that
if ![]() and
and ![]() are independent with
are independent with
![]() and
and
![]() , then
, then
![]() .
For example, the sum
.
For example, the sum ![]() of
of ![]() independent rainfall totals
distributed as
independent rainfall totals
distributed as
![]() will also be Gamma
distributed as
will also be Gamma
distributed as
![]() .
.
Several commonly used distributions are special cases
of the gamma distributions.
The exponential distribution
![]() is the
special case of the Gamma distribution when
is the
special case of the Gamma distribution when ![]() i.e.
i.e.
![]() .
The special case
.
The special case
![]() is also known as
the chi-squared distribution
is also known as
the chi-squared distribution
![]() with
with
![]() degrees of freedom.
The chi-squared distribution describes the distribution
of the sum of squares of
degrees of freedom.
The chi-squared distribution describes the distribution
of the sum of squares of ![]() independent standard normal
variables, and so for example, the sample variance of
independent standard normal
variables, and so for example, the sample variance of
![]() independent normal variates is distributed as
independent normal variates is distributed as
![]() (there are
(there are ![]() degrees
of freedom rather than
degrees
of freedom rather than ![]() since one is lost in estimating
the sample mean).
since one is lost in estimating
the sample mean).