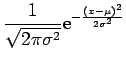 |
(4.7) |
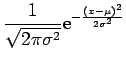 |
(4.7) |
The reason why the normal distribution is so effective at explaining many measured variables is explained by the Central Limit Theorem, which roughly states that the distribution of the mean of many independent variables generally tends to the normal distribution in the limit as the number of variables increases. In other words, the normal distribution is the unique invariant fixed point distribution for means. Measurement errors are often the sum of many uncontrollable random effects, and so can be well-described by the normal distribution.
The standard normal distribution with zero mean and unit
variance
![]() is widely used in statistics. The
area under the standard normal curve,
is widely used in statistics. The
area under the standard normal curve, ![]() , is sometimes referred
to as the error function and given its own special symbol
, is sometimes referred
to as the error function and given its own special symbol ![]() ,
which can be evaluated numerically on a computer to find probabilities.
For example, the probability of a normally distributed variable
,
which can be evaluated numerically on a computer to find probabilities.
For example, the probability of a normally distributed variable ![]() with mean
with mean ![]() and
and ![]() being less than or equal to
being less than or equal to
![]() is given by
is given by
![]() , which is equal to
, which is equal to
![]() .
.