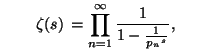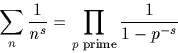Prime Evolution Notes

[original version - posted 23/11/00]

Here's the updated version of these notes [15/9/00]

Warning: The contents of this document are extremely vague! This is an unavoidable consequence of (1) the unorthodox nature of the material and (2) my relative unfamiliarity with many of the technical issues involved, and general reliance on intuition. You might notice some unfamiliar terminology which I've introduced simply because I wasn't aware of any existing terms which would apply. Please do not be put off by this. In fact, rather than approaching this as a coherent whole, I suggest you see it as a loose collection of curious notions, amongst which there may be one or two useful new ideas. If you wish to demonstrate that this is all nonsense (and you may be right - I just don't know), then you are invited to explain why for the benefit of myself and others.

Table of Contents

1.1 An evolving sequence {q_n(t)} in R⁺, at each time t, generates a 'multiplicative closure' - the set of all finite products of q_n(t)'s, including the 'null product', or 1. This obviously embeds the sequence {q_n(t)}.

1.2 The primes are unique among such sequences in that their multiplicative closure (i.e. N) is equally-spaced (or equivalently, additively closed) and 'non-intersecting'. Note that any set of natural numbers containing all of the primes generates an equally-spaced closure.

1.3 (QUESTION)When does the sequence {q_n} have a multiplicative closure with asymptotic density equal to 1? i.e. is there a simple way to characterise the set of such sequences? (The reasons for asking this question will become clear. Personally, I'd guess that there may be some involvement of the set LD discussed in Section 4.)

1.4 Suppose we devise a dynamical system where the evolution of a sequence is in some sense 'caused' or 'driven' by the unevenness of the spacing in its multiplicative closure. The idea is that the sequence of primes is a unique 'balanced' or 'equilibrium' state, an 'attractor' where the forces responsible for the evolution vanish. Through a sort of 'self-organising feedback loop', a sequence might then evolve towards 'primeness' and stop when it reaches this state (where all q_n(t) = p_n). We can think of 'primeness' in this situation as a kind of arithmetic equilibrium' where addition and multiplication are in harmony with each other, characterised by the geometric regularity of the multiplicative closure.

1.5 One possible scheme involves treating the sequence as a set of charged particles moving in a fixed 1-dimensional field. The charges on the particles fluctuate deterministically based on the multiplicative closure at each time t.

The charge on a particle would perhaps be given by an infinite sum of weighted contributions from each of its 'multiples' in the closure. Larger multiples would make proportionally smaller contributions, in such a way that these charge-sums are finite. The contributions would be based on some kind of 'density' measurable at each point in the closure. Each multiple can be thought of as 'trying to influence' each of its factors in such a way as to appropriately increase or decrease the density at its location. The process would continue until uniform density were achieved throughout the closure, i.e. when the sequence generating it had been forced into a state of 'primeness'.

1.6 Originally I'd thought of point-charge particles (with fixed charges) in a responsively fluctuating field, but for various reasons I now think that the idea of fluctuating charges in a fixed field is more plausible.

1.7 The idea of charged particles suggests further forces due to inter-particle interaction. If this were involved, it is unclear whether it would be inverse-square-based mutual repulsion, something logarithmic (where particles were mutually attractive at long range and mutually repulsive at short range), or something altogether different. Also there is the issue of whether it should be a 'nearest neighbour' interaction or a universal interaction.

1.8 The pole s = 1 of the zeta function would presumably be some kind of singularity in the field in which the particles are moving. Could the presence of such a field be related to time-irreversibility (as required of the 'Riemann dynamics' which Berry, et.al. seek)? In the various billiard models, an external magnetic field is generally introduced to bring about time-irreversibility.

1.9 Just an intuition: Discrete Fourier analysis applied to the multiplicative closure may be of some use in defining charges on the sequence of particles.

1.10 Another, rather naive, approach is to define a counting function c(x) on the multiplicative closure, and then use the fluctuations c(x)-x to define the 'density' which is needed to define charges on the sequence of particles. c(x)-x simply measures whether there have been too many or not enough elements of the multiplicative closure in the interval (0,x).

[Contents]

2.1 Imagine the primes as a sequence of particles occupying positions {p_n} in a 1-dimensional field. Now imagine these particles being perturbed, or moving slightly. We can then simply adapt Euler's infinite product

to arrive at the idea of 'modified zeta functions', which evolve continuously with a continuously evolving sequence of particles. These functions may have been studied already. In any case, a few questions come to mind:

2.2 (QUESTION) For what class of sequences will the corresponding modified zeta functions have range of convergence (1,infinity), like the usual Riemann zeta function?

2.3 (QUESTION) For what class of these sequences (2.2) will the corresponding modified zeta functions allow analytic continuation to C\{1}?

2.4 (QUESTION) For what class of these sequences (2.3) will the corresponding (analytic continuations of the) modified zeta functions have simple poles at s = 1 ?

2.5 (QUESTION) For what class of these sequences (2.4) will the corresponding modified zeta functions produce sets of 'trivial' zeros on the negative real axis?

2.6 (QUESTION) For what class of these sequences (2.5) will the corresponding modified zeta functions also produce sets of 'nontrivial' zeros contained within the critical strip 0 <Re s < 1 ?

2.7 (QUESTION) For what class of these sequences (2.6) will the corresponding modified zeta functions produce sets of 'nontrivial' zero symmetric with respect to the critical line Re s = 1/2 ?

2.8 (QUESTION) For what class of these sequences (2.6) will the corresponding modified zeta functions produce sets of 'nontrivial' zeros with GUE-like spacing statistics ? (The usual zeta function has this property. GUE = Gaussian Unitary Ensemble. See http://match.stanford.edu/rh/gue.htm)

2.9 (QUESTION) Consider how the prime-counting step functionpi( x) can be expressed as a limit of sums of smooth functions based on powers x^(rho_j) where rho_j are the nontrivial (complex) zeros of the usual zeta function. Suppose then that we 'perturb' the primes slightly to produce a sequence {q_n}. This generates both a modified step function (counting the {q_n}), as well as a modified zeta function with a new set of complex zeros. Under what conditions can we guarantee that the analogous limit function, built from powers of x where the exponents are the modified nontrivial zeros, will coincide with the modified step function?

2.9 Note how a modified zeta function relates a sequence to its multiplicative closure via the analog of the usual formula

which relates the sequence of primes to its multiplicative closure, N.

2.10 Corresponding to an evolving modified zeta function, we have an evolving set of zeros in C. It seems possible that by making the appropriate restrictions on the evolution of the sequence, we can guarantee the 'nontrivial' zeros are in the critical strip, or perhaps even on the critical line. Suppose the Hilbert-Polya conjecture is correct, and the complex zeros of the usual zeta function do replicate the spectrum of eigenvalues of a Hermitean operator on a Hilbert space. We might then consider in what ways we can modify the primes so that the evolving set of zeros in C continues to correspond to the spectrum of such an operator, for each time t. This leads us to the idea of an evolving operator...

[Contents]

3.1 The last section concluded with the (rather nonlinear) idea of a quantum system where the operator evolves with the evolution of the state vector. Someone has almost certainly developed this idea if indeed it can be given a precise meaning. We shall proceed under the assumption that it can.

3.2 An evolving operator will give us an evolving spectrum of eigenvalues. Therefore in certain situations, an evolving operator will correspond to an evolving modified zeta function (whose nontrivial zeros match the spectrum of the operator at each time t).

3.3 The hypothesised Hilbert-Polya operator, which would prove the Riemann Hypothesis, might then be the 'final state' of the evolving operator. An evolving sequence has reached 'primeness' or 'arithmetic harmony' as described earlier, and stopped evolving. Its evolution generated an evolving modified zeta function, which corresponded to an evolving operator, as describe in the previous note. At the moment the sequence stopped, the operator was fixed at one particular 'value'. Could the Hilbert-Polya operator possibly be something like this?

3.4 This brings us to the idea of a kind of feedback loop. Although there is no one method for determining a quantisation of a classical (Hamiltonian) system, the reverse process is straightforward - replace the noncommutative operators associated with the physical observables by simple commuting variables. In this way, a feedback could possibly be introduced. The "evolving operator" discussed above would give rise to an evolving underlying classical Hamiltonian. This could possibly "drive" the evolution of the sequence. The idea is summarised informally in the following "causative loop":

Sequence evolves -- > Modified zeta function evolves --> set of zeros in C evolves -- > corresponding operator evolves --> "underlying" Hamiltonian evolves --> sequence evolves according to Hamiltonian at each moment

Could this be in some way compatible with the arithmetic dynamics described in Section 1?

3.5 Recall that the prime-counting step function pi(x) can be represented as an exact limit of smooth functions, using the nontrivial zeros of the Riemann zeta function. The zeros of modified zeta functions could, under certain conditions, be used to construct analogous limits, which would be modifications of pi(x). These would not necessarily be step functions.

Recall that pi'(x), the 'density of primes' function, is just a sum of Dirac delta functions

The derivative pi'(x) of the modified pi(x) could possibly blur out into a much less discrete density (distribution). This suggests that it may be appropriate to allow the 'particles' to (individually) be 'distributed objects' in some context. This might relate to some kind of quantisation of the arithmetic dynamics.

3.6 If, due to quantisation, we had probability densities rather than actual positions for the particles, the semiclassical limit should produce Dirac delta functions, in accordance with the density function pi'(x).

3.7 If the imaginary parts of the nontrivial zeros rho_j are to behave like eigenvalues, we might consider what the corresponding eigenstates (base states) could be. Consider the expansion

where R is the Riemann function, and rho the complex zeros of the zeta function. (Could this identity be a dynamical law which holds throughout the evolutionary process?)

So the prime density fluctuation function D(x) = pi(x) - R(x) will be an infinite sum of 'exponential rescalings' of the Riemann function R. It is quite remarkable that a single smooth function can provide not only an excellent estimate for pi(x), but also, through an infinite sum of these 'rescalings', an exact expression for the remainder (density fluctuation function) pi(x) - R(x).

It would seem that the base states are going to relate somehow to the various rescalings of R, or 'prime harmonics'.

A graph of the prime density fluctuation function D(x) from [GHR]. This seemingly "noisy signal" can be decomposed into "harmonics" corresponding directly to the zeta zeros. Michael Berry has often used a musical analogy.

3.8 Presumably, if the arithmetic dynamics could be modeled, there would be a phase space involved. In a Hamiltonian setting, this would normally be considered as the union of constant energy surfaces, on which conservative systems evolve. If total energy was the sum of kinetic and potential energies in the arithmetic dynamics, then due to the unusual nature of the dynamics, I suspect the potential energy would be quite difficult to define.

Also, the arithmetic dynamics need not be conservative. In [GHR], the authors calculate the four Liapunov exponents of the prime density fluctuation function, arriving at a sum of -0.07. As there is a margin of error involved, and this sum is reasonably close to zero, the authors safely conclude that the "unknown dynamical system" associated with the prime distribution could be either conservative or dissipative.

Note that the authors were approaching the prime distribution from the point-of-view of interested chaos theorists. They applied a technique to the primes which is normally applied by physicists to experimental data generated by a (possibly unknown) dynamical system, to determine if it is chaotic, etc. It seems that they were not (consciously) suggesting that the primes are the result of some dynamical evolution, as I am here.

[Contents]

4.1 In his paper [W], Marek Wolf shows that the primes, treated as a signal, display 1/f noise (this is a form of self-similarity). It turns out that it is a consequence not of the arithmetic 'primeness' of the primes, but of the fact that they are distributed with a density asymptotic to x/log x. Any such sequence will show 1/f noise when considered in the same way. This points to a surface (which I call LD) of 'logarithmically distributed' sequences in whichever sequence space we are using.

4.2 In [BTW] Per Bak, Chao Tang, and Kurt Wiesenfeld demonstrated a link between 1/f noise and self-organising systems. Wolf cites this, and it inspired the extraordinary concluding question "Are the prime numbers in a self-organized critical state?" Although this is not meant to be more than speculation, reading it made me feel that my strange 'evolutionary' ideas might not be completely meaningless.

4.3 More information and some useful links relating to1/f noise and self-organising critical systems can be found here.

4.4 Note that 1/f noise appears in physical systems as diverse as sunspots, quasars, hourglasses, rivers, electronic components, economies, DNA codes, speech and written language. Bak, et.al. imply that all of these are in some sense self-organising. They put forward a simple model (what's become known as the "sandpile dynamics") to suggest how this might be possible. However, an earlier model they propose in [BTW], involving a sequence of nearest-neighbour interacting torsion-pendula, may be more immediately compatible with these ideas.

4.5 As I have been assembling this web document, it has occured to me that the 'sandpile dynamics' may be directly involved in the evolutionary dynamics underlying the primes. The idea is to look at gaps between consecutive primes, and their deviations from the local average. These values can then be treated as 'heights' of a 1-dimensional sandpile at each position.

The sandpile dynamics might have to be adapted so that 'continua' rather than 'quanta' of sand flowed from one position to its neighbours, and so that the mechanism governing this was probabilistic rather than deterministic. In this way, the 1-dim. sandpile would be seen to gradually 'level itself out' or approach equilibrium, corresponding to an LD sequence. The arithmetic forces could then be responsible for the finer points of the distribution.

4.6 One obstacle is that Bak, Tang and Wiesenfeld suggest 1/f noise is a temporal fingerprint of self-organising criticality, and self-similarity is the spatial fingerprint. The 1/f noise in the primes would appear to be more of a spatial than a temporal matter. However, the ideas of 'space' and 'time' are somewhat ambiguous in the context of an evolutionary dynamics which somehow generates the prime distribution. Also, in some of the examples of 1/f noise (see Wentian Li's extensive 1/f Noise Bibliography) it's hard to see how the noise could be a temporal attribute.

This brought to mind the curious quotation from J.J. Sylvester:

"I have sometimes thought that the profound mystery which envelops our conceptions relative to prime numbers depends upon the limitations of our faculties in regard to time, which like space may be in essence poly-dimensional and that this and such sort of truths would become self-evident to a being whose mode of perception is according to superficially as opposed to our own limitation to linearly extended time."

from Collected Mathematical Papers, Volume 4, page 600

which in modern English says something like:

"I have sometimes thought that the profound mystery of the distribution of prime numbers only seems mysterious to us because of our limitations in perception related to time. Time, like space, may be multi-dimensional, and perhaps to a being who could perceive a more generalised kind of time there would be no mystery surrounding prime numbers - it would all be obvious."

4.7 In a personal communication, Michael Berry stated that he thought the 1/f noise in the primes was "not fundamental" and only due to a "failure to rescale the primes so that their mean spacing is zero". He pointed out that once rescaled, "the fluctuations separate cleanly from the mean density, and have Poisson character (apart from fine-scale arithmetic features such as that embodied in the Hardy-Littlewood conjecture)".

With the utmost respect to Professor Berry, I think that he might be overlooking the point of what Wolf has discovered. I can see the value of rescaling spectra of energy levels, etc. and studying their statistics. Looking at the statistics of the rescaled nontrivial zeta zeros has proven similarly rewarding. But why dismiss a potentially crucial result due to a "failure to rescale"? The primes, in their natural state, show a very particular kind of logarithmic density, which is mathematically linked to the remarkable and ubiquitous phenomenon of 1/f noise. This may be coincidental, but it's at least worth considering, especially with all of the emerging, and largely mysterious links between primes and various aspects of modern physics.

4.8 I suspect that the surface LD in sequence-space may be related to the answers of some of the "modified zeta function" questions in Section 2. That is, the LD surface may be the appropriate place for the evolution to occur. If this is the case, it is somewhat reminiscent of a conservative Hamiltonian system evolving on a fixed energy surface in phase space. However, I can't see how the two notions could be reconciled (unless a radically different kind of "energy" were defined, or perhaps if the dynamics were based on the conservation of some entirely different quantity.)

4.8 Note that you can replace any finite portion of any sequence in LD and it will remain in LD.

4.9 Within LD, the sequence of primes obviously distinguishes itself. This distinction can be represented by the deviations of the primes from the asymptotic logarithmic density. The above diagram from [GHR] illustrates these deviations, as does the 'scattering' around the base of the curves in Figure 2 of [W]. They are directly related to the zeros of the Riemann zeta function.

4.10 On page 368 of [BTW], the authors explain that "Once relaxed, the properties of the [self-organised critical] state are probed by locally perturbing the system." If the primes are in a self-organised critical state, as Wolf hints, then we might try to imagine the result of this kind of probing. Periodic orbits of the underlying classical system should be multiples of {log p_n}. Could these relate to the results of a post-evolutionary "probing" of the prime distribution, involving the perturbation of individual primes?

[Contents]

5.1 In his article [J], Bernard Julia constructs the free Riemann gas whose particles are the primes {p_n}, with energies {log p_n}. The construction is quite simple and uncontrived. Using fermionic statistics and considering the grand canonical ensemble, he is able to show that its partition function is the Riemann zeta function. Here the number of particles N is allowed to vary freely in the ensemble and volume V is not involved. Temperature T is the only parameter of the partition function, in the form x = 1/T, where x is the parameter of the real-valued zeta function.

5.2 Since the seminal paper of Lee and Yang [LY], the extension of partition functions to the complex plane, and the study of their zeros has been commonplace. Julia points out that "Lee-Yang type theorems restrict the locus of zeros of partition functions that may be related to phase transitions. The Riemann Hypothesis is similar." He also relates the pole of the Riemann zeta function at s = 1 to something known as a Hagedorn catastrophe.

5.3 As the spectrum of allowed energies over the ensemble is {log n : n=1,2,3...}, the partition function is basically providing a probability distribution over the natural numbers for each x in the interval (1,infinity). Recall that a partition function 'divides up' a unit of probability between all allowable energies, based on the proportion of the systems in the ensemble which possess each energy. Although it is not clear what these probabilities refer to in the context of [J], I suspect that they might be involved in what I'm trying to achieve.

5.4 Representing the distribution over N as the partition of a vertical unit into sections corresponding to the sequence of probabilities, and placing these vertical units above each x on the horizontal axis, a sequence of curves emerges, the first few illustrated below:

Equivalently, we can consider the individual functions

p_n(x)=1/(zeta(x) n^x) = probability of n 'occurring' at (inverse 'temperature') x

Again, it's not clear what the 'occurring' means here. Julia seems to be ambiguous on this point (or there is some subtlety I have missed).

We find that the maxima m_n of these functions tend slowly towards 1. Some examples:

m₂ = 1.8791006…, m₃ = 1.6351665…, m₄ = 1.5329592…, m₅ = 1.4743970…

m₁₀ = 1.3740486…, m₂₀ = 1.3696203…, m₃₀ = 1.3692338…, m₄₀ = 1.3690822…

The areas under these curves are finite, so we could normalise and arrive at a sequence of probability densities, one for each n over the interval (1,infinity). It's not clear whether this would be helpful or actually refer to anything, but it's worth a mention.

If these probability densities are saying anything, it is (loosely speaking) this:

In some unknown context, n = 1 is certain to 'occur' at absolute zero temperature (T = 0, so x is infinite), and all other natural numbers n are most likely to 'occur' near 1, with larger numbers tending to 'occur' closer and closer to 1.

Obviously this is a complete inversion of where the natural numbers actually occur on the number line.

5.5 Note that modified zeta functions (see Section 2), which result from perturbing the primes, will give modifications of the 'Julia partitions' for each x. Hence the individual probability density functions p_n(x) described above could be seen as evolving.

5.6 The idea of probability density functions associated with individual numbers might somehow relate to the quantisation of the evolutionary dynamics (if indeed such a thing can be defined).

5.7 There have been several recent variations on Julia's free Riemann gas concept:

• In a recent lecture in Budapest, Marek Wolf introduced a "prime gas" where energies are based on the gaps between primes, rather than on their actual magnitudes. In this way, his thermodynamics involves something like a volume V, which [J] fails to do. In Wolf's gas, the partition function suggests that the primes behave like noninteracting harmonic oscillators.
• In [BC] Jean-Benoit Bost and Alain Connes describe a dynamical system (in C* algebra formalism) whose partition function is zeta, and where the pole at s = 1 corresponds to a spontaneous breaking of symmetry.
• D. Harari and E. Leichtnam generalise this to the general number field case in [HL].
• In [C], Paula Cohen improves on [HL] by presenting a generalisation whose partition function is the Dedekind zeta function corresponding to the number field in question.

[Contents]

6.1 Much work has been done by Andrew Odlyzko, Michael Berry and others to demonstrate the similarity between the Gaussian Unitary Ensemble eigenvalue spacing statistics and the statistics of the nontrivial zeta zero spacing. One blatant similarity is the following pairwise correlation function which applies in both settings:

Here g(r) is the probability that you will find another eigenvalue (zero) a distance r away from a given eigenvalue (zero). This formula had been discovered in the context of random matrix theory by Freeman Dyson, and separately for zeta zero statistics by Hugh Montgomery. They coincidentally became aware of the similarity in each others' work in 1972. A graph of g(x) looks like this:

It is often said that this suggests a 'repulsion' between zeros, unlike the Poisson spacing statistics. If we imagine that the prime distribution is the result of an evolutionary process, then the zeta zeros will be the result of an accompanying 'dual' evolution (see Section 2).

Could this 'repulsion' evident in the 'final state' of the zeta zeros' evolution somehow reflect some repulsive quality in the evolutionary dynamics (and/or its dual)?

6.2 The GUE is an ensemble, that is, a space of unitary matrices together with a particular probability density. Matrices in the GUE are often referred to as 'random matrices'. Although such statements can be made rigorous, there is a subtlety here that should not be overlooked. An individual matrix with fixed entries can never be 'random'. The randomness is only present in the wider context of the probability density over the entire ensemble.

The statistics discussed in 6.1 relate to the behaviour of eigenvalues of matrices taken at random from this ensemble. It is not difficult to make precise and meaningful statements about this. Now if it exists, the hypothetical Hilbert-Polya operator is one fixed operator, it cannot be 'random', yet it is often said that it behaves like an (arbitrarily large) random unitary matrix. Such statements are based on the remarkable correspondence of statistical properties discussed above.

To me, this suggests that the statistics of the zeta zeros are a clue to some kind of (evolutionary) 'history' associated with the zeta function, and the related Hilbert-Polya operator. For the connection with the GUE 'points to' or 'implies' an entire class of operators, suggesting that the operator we're looking for has taken other "values" in the "past". The GUE probability density could then be a clue as to the actual dynamics governing the evolution. It seems to suggest that the evolving Hermitean operator is more likely to take some values than others, in a very particular way.

[Contents]

7.1 It had occurred to me that Dirichlet series are some kind of hyperbolic or logarithmic generalisation of Fourier series, in then following sense

{Sum over n}a_n /n^x can be rewritten as

{Sum over n}a_n* exp[i(i log n)x] which equals

{Sum over n}a_n * [cos(i log n)x + sin (i log n)x], or

which could be then be expressed in terms of cosh and sinh.

This suggested that Dirichlet series are in some sense analogous to Fourier series, but concerned with periodicities on a logarithmic scale (i.e. self-similarity). I wondered if an analogous 'Dirichlet analysis' had been developed. Julia pointed out to me recently that this is all made explicit in Hardy and Wright's book [HW].

Note that (1) the Riemann zeta function is the archetypal Dirichlet series (all coefficients equal 1), and (2) the decomposition of pi(x)-R(x) into 'prime harmonics' discussed in Section 3 is reminiscent of a Fourier decomposition, but dealing with different scaling regimes rather than with periodicities.

Also note that Marek Wolf has discovered at least three different kinds of self-similarity within the distribution of primes.

7.2 It's important to understand the role of the logarithm function in relating the continuum to the half-continuum. The log function obviously maps the half interval (0,infinity) onto the real line in such a way that the multiplicative identity 1 gets mapped to the additive identity 0. The reason that the primes are logarithmically 'spaced out' would appear to be closely linked to the fact that the domain in which they exist has an edge (i.e. they live in a half-continuum).

It may also be of some interest to note that the graph of y = log x is one of the simplest self-similar objects which can be constructed. Its self-similarity is evident when you rescale the x-axis, and the graph simply 'scrolls' up or down parallel to the y-axis.

7.3 I suspect that following mathematical structures may also be of some use: Clifford algebras (particularly David Hestenes' closely related geometric algebras of arbitrary dimension), unique factorisation domains, p-adic numbers.

[Contents]

8. General physics clues

8.1 The possibility of nearest-neighbour interaction in the hypothesised "arithmetic dynamics" described in Section 1 above brings to mind lattice gases, Ising models, and the Bak-Tang-Wiesenfeld torsion pendulum model (see [BTW]).

Also, Wolf and Julia have pointed out that the Kramers-Wannier duality [KW], which relates to Ising models and lattice gases, parallels the zeta function's functional equation

8.2 For many years, Andrew Odlyzko has been developing algorithms for computing zeros of the Riemann zeta function. At the time of writing of [O], his fastest algorithm was "very similar to the one proposed by Greengard and Rokhlin [GR] for astrophysical many-body simulations, and could be used in its place."

8.3 Freeman Dyson [D] linked random matrices and Brownian motion. Patrick Billingsley [B] linked Brownian motion and prime numbers, and more recently H.Gopalkrishna Gadiyar and R. Padma [GP] have linked the Wiener-Khintchine formula to the distribution of prime pairs. This formula is normally applied in the modelling of Brownian motion (among other physical phenomena).

As discussed in [BK] random matrices are linked to the primes through the GUE spacing statistics of the nontrivial zeros of the Riemann zeta function. This is absolutely central to the 'spectral interpretation' approach to the Riemann hypothesis.

Is this "triangle of relationship" fully understood? Or does Brownian motion have some role to play in the evolutionary dynamics?

[Contents]

9. Other ideas for dynamics

9.1 The evolutionary dynamics could perhaps be modeled in such a way that the process had a very definite starting point. It might be possible to introduce something analogous to the "big bang", where all of the particles begin at a single position (say at 1). Some infinitesimal perturbation, together with a mutual repulsion between the particles, might then result in an "explosion" in the positive direction. This could initiate the evolutionary process which terminates with the familiar distribution of prime numbers. The immediate obstacles to giving this a coherent mathematical description might be overcome through the application of non-standard analysis.

9.2 Evolution might not be based on conservation of energy (as in usual Hamiltonian mechanics) but conservation of some other quantity. If LD does turn out to be an appropriate surface on which evolution could occur, could it be a surface on which some quantity was preserved? What, if anything, could this other quantity be? What is preserved when a sequence evolves on LD?

9.3 Evolution in a lattice rather than a continuum?

9.4 Evolution in C rather than in R⁺?

9.5 If we also consider the set of inverse primes {1/p_n} in the interval (0,1) as part of the dynamics, then the multiplicative closure will be ideally evolving towards the positive rational numbers Q⁺ rather than towards N. Could something from measure theory be applied to the closure in this situation, in order to define charges on our particles in a way which would work? Is there some sense in which Q⁺ has a 'uniform density' but a general multiplicative closure does not?

[Contents]

10. Miscellaneous questions

10.1 Does the truth of the Riemann Hypothesis imply the existence of a Hilbert-Polya operator? (i.e. is the converse of Hilbert and Polya's observation known to be true?)

10.2 Repeated application of the Riemann zeta function to the interval (1,infinity) leaves the point 1.83377... fixed. What else does it do? Some kind of stretching/compression, presumably?

10.3 Has anyone looking at the primes from a thermodynamic viewpoint attempted to apply the concept of entropy?

10.4 Is there a simple way to compute the trivial zeros of a modified zeta function? Can the evenly-spaced nature of the trivial zeros of the Riemann zeta function be seen to be directly linked to the evenly-spaced nature of the multiplicative closure of the primes (i.e. N) in the wider context of modified zeta functions? (see section 2)

[W] M. Wolf, "1/f noise in the distribution of prime numbers", Physica A, 241 (1997) 493-499.

[GHR] Z.Gamba, J.Hernando and L.Romanelli, "Are the prime numbers regularly ordered?", Physics Letters A 145, no.2,3 (1990) 106-108.

[HW] G.H. Hardy and E.M. Wright, An Introduction to the Theory of Numbers, Clarendon Press, Oxford (1945)

[BTW] P.Bak, C. Tang and K. Wiesenfeld ,"Self-organized criticality", Physical Review A, 38, no.1 (1988) 364-374.

[J] B. Julia, "Statistical theory of numbers" from Number Theory and Physics (Springer Proceedings in Physics, Volume 47. editors Luck, Moussa and Waldschmidt, 1990)

[BC] J.-B. Bost and A. Connes "Hecke Algebras, Type III factors and phase transitions with spontaneous symmetry breaking in number theory," Selecta Mathematica (New Series), 1 (1995) 411-457.

[HL] D. Harari and E. Leichtnam, "Extension du phenomene de brisure spontanee de symetrie de Bost-Connes au cas des corps globaux quelconques," Selecta Mathematica, (New Series), 3 (1997) 205-243.

[C] P. Cohen "Dedekind zeta functions and quantum statistical mechanics" (ESI preprint).

[LY] T. Lee and C.Yang, "Statistical theory of equations of state and phase transitions", Physical Review, 87, no.3 (1952) 404-419.

[KW] H.A.Kramer and G.H.Wanier, "Statistics of the two-dimensional ferromagnet. Part I", Physical Review 60 (1941) 252-.

[O] A. Odlyzko, "Primes, quantum chaos, and computers"

[GR] L. Greengard and V. Rokhlin, "A fast algorithm for particle simulations", Journal of Computational Physics, 73 (1987) 325-348.

[D] F.J. Dyson, "A Brownian-motion model for the eigenvalues of a random matrix", Journal of Mathematical Physics, 3 (1962), 1191-1198.

[B] P. Billingsley, "Prime numbers and Brownian motion", American Mathematical Monthly, 80 (1973) 1099-1115.

[BK] M.V. Berry and J.P. Keating, "The Riemann zeros and eigenvalue asymptotics", SIAM Review, 41, No.2 (1999), 236-266.

[GP] H.Gopalkrishna Gadiyar and R.Padma, "Ramanujan-Fourier series, the Wiener-Khintchine formula and the distribution of prime pairs", Physica A 269 (1999) 503-510.