---

Selberg trace formula and zeta functions

---

G. Mackey, from Unitary Group Representations in Physics, Probability,and Number Theory (Benjamin/Cummings, 1978) p.324    [continued discussion]

[This is the rational (simplest) case of A. Weil's 1952 generalisation of the (number theoretical) explicit formula of Riemann and von Mangoldt. Here h is a complex-valued function of a real variable which satisfies certain conditions, and g is an integral transform of h. Further notes on this formula can be found here. It is very similar in form to a particular case of Selberg's trace formula.]

where the nontrivial zeros of the Riemann zeta function are denoted by

  ^"

D. Hejhal, The Selberg Trace Formula for PSL(2,R) - Volume I, p. 35

"Selberg noticed this similarity...and was quickly led to a deeper study of trace formulas. Among other things, Selberg found that there is a zeta function which corresponds to [his trace formula] in the same way that [the Riemann zeta function] corresponds to [the Riemann-Weil explicit formula]. This zeta function is nowadays referred to as the Selberg zeta function; it is usually denoted by Z(s)."

D. Hejhal, "The Selberg trace formula and the Riemann zeta function", Duke Mathematics Journal 43 (1976) p.459

"Motivated by the mysterious resemblance of the Selberg trace formula to this explicit formula, Selberg introduced [the Selberg zeta function:]

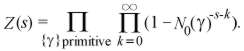
Its zeros are s with s(1-s) an eigenvalue of [the Laplace-Beltrami operator], so Z(s) = 0 implies s = 1/2 + it, t real or s in [0,1]."

D. Bump, "Spectral Theory of SL(2,R)" (Jerusalem 2001 lecture notes)

"Besides a series of 'trivial' roots, all the roots of Selberg's zeta function fall on the line 1/2 + iR: in fact they are precisely the numbers 1/2 + ik for which -(1/4 + k) ² is an eigenvalue of [the Laplacian]. This is the 'Riemann conjecture' in the present case."

H.P. McKean, "Selberg's trace formula as applied to a compact Riemannian surface", Communications in Pure and Applied Mathematics 25 (1972) 225-246.

"The Selberg trace formula was originally introduced as an arithmetical relation, being a noncommutative generalisation of the Poisson summation formula, and it is used as such in number theory and harmonic analysis. In the present context we view it as an identity relating dynamical quantitities, the quantal spectrum of the Laplace-Beltrami operator and the classical 'length spectrum' of periodic geodesics, both being defined on a configuration space of the form D/G."

A. Voros and N.L. Balasz, "Chaos on the pseudosphere", Physics Reports 143 no. 3, p. 169.

"On a compact (i.e. closed and bounded) two-dimensional surface of negative Gaussian curvature the classical motion [of a point mass] takes place on the geodesics, and it is as chaotic and nonintegrable as possible (being Bernoullian). On this surface there exists also a well-defined quantum dynamics, where the Laplace-Beltrami operator (the invarian Laplacian) acts as the Hamiltonian in the Schrödinger equation. A limiting procedure, exactly parallel to the semiclassical tradition in ordinary quantum mechanics, takes the quantum theory into the classical one when the energy E becomes large, E^-1/2 playing the role of Planck's constant...(We note that the general "inverse problem" of quantising classical mechanics on a curved space, which presents its own difficulties of another order, does not arise here.) If in addition the curvature is constant, this semiclassical transition is even understood in a certain sense, exemplified by the Selberg trace formula [5]. This formula, which was motivated by Riemann's zeta function, relates in an exact way the spectrum of the quantal motion on compact surfaces of negative curvature to the classical motion. The so-resulting mathematical literature [6] has deep connections with manifold theory, automorphic functions, number theory, etc.; however, it does not address itself explicitly to questions which are of crucial interest to the physicist, i.e., the detailed properties of the discrete energy spectrum and associated eigenfunctions, and their relation to questions of quantum ergodicity and quantal chaos.

Physicists were not much concerned by the purely classical aspects of this model. For them ergodicity and mixing were the consequence of forces of interaction between particles, and not of physically nonrealisable constraint forces. However the situation becomes different if we view this as an exactly soluble classical model to be quantised, in order to study quantum-mechanically the manifestation of chaoticity. Nevertheless, very little use has been made of this model. In effect, only two pioneering studies have appeared in this direction until now. Gutzwiller [7] has drawn attention to the relation between Selberg's trace formula and the semiclassical expansion of Green's function described by a path integral. He also studied [8] the scattering on a compact surface of constant negative curvature using the work of Lax and Phillips [9]."

A. Voros and N.L. Balasz, "Chaos on the pseudosphere", Physics Reports 143 no. 3, p. 112.

[5] A. Selberg, "Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series", Journal of the Indian Mathematical Society 20 (1956) 47-87.
[6] Hejhal, D., The Selberg Trace Formula for PSL(2,R), Volume I (Springer Lecture Notes 548, 1976)
[7] M.C. Gutzwiller, Physical Review Letters 45 (1980) 150-153.
[8] M.C. Gutzwiller, Physica D 7 (1983) 341-355.
[9] P.D. Lax and R.S. Phillips, Scattering Theory for Automorphic Functions (Princeton University Press, 1976)

"The classical periodic orbits are a crucial stepping stone in the understanding of quantum mechanics, in particular when then classical system is chaotic. This situation is very satisfying when one thinks of Poincaré who emphasized the importance of periodic orbits in classical mechanics, but could not have had any idea of what they could mean for quantum mechanics. The set of energy levels and the set of periodic orbits are complementary to each other since they are essentially related through a Fourier transform. Such a relation had been found earlier by the mathematicians in the study of the Laplacian operator on Riemannian surfaces with constant negative curvature. This led to Selberg's trace formula in 1956 which has exactly the same form, but happens to be exact. The mathematical proof, however, is based on the high degree of symmetry of these surfaces which can be compared to the sphere, although the negative curvature allows for many more different shapes."

M.C. Gutzwiller, "Chaos in Quantum Mechanics" (1998 lecture notes)

extensive notes from Gutzwiller on the Selberg Trace Formula and quantum chaos

H.-J. Stöckmann, Quantum Chaos: An Introduction (Cambridge Univ. Press, 1999)

[This contain a physics-based approach to the Selberg trace formula.]

Unfortunately there are few good references on the Selberg trace formula. Peter Perry suggested the following:

H.P. McKean, "Selberg's trace formula as applied to a compact Riemannian surface", Communications in Pure and Applied Mathematics 25 (1972) 225-246. See also the relevant erratum in Comm. Pure Appl. Math. 27 (1974) p.134.

"This will give a somewhat breezy but in principal complete derivation of Selberg's trace formula for a compact Riemann surface - where the Laplacian has only eigenvalues and no continuous spectrum. There are generalizations to cases where the underlying manifold is non-compact and the Laplacian has continuous spectrum, but these are much more involved analytically.

and so relates the test function evaluated at lengths on the left to its Fourier transform evaluation at square roots of eigenvalues on the right).

Selberg's trace formula is the spiritual ancestor of the celebrated Duistermaat-Guillemin trace formula. See:

J. Duistermaat and V. Guillemin "The spectrum of positive elliptic operators and periodic bicharacteristics", Invent. Math. 29 (1975), no. 1, 39-79."
 

A. Selberg, "Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series", Journal of the Indian Mathematical Society 20 (1956) 47-87.

This is the article in which the trace formula first appeared:

[abstract] "In the following lectures we shall give a brief sketch of some representative parts of certain investigations that have been undertaken during the last five years. The center of these investigations is a general relation which can be considered as a generalization of the so-called Poisson summation formula (in one or more dimensions). This relation we here refer to as the "trace-formula.""

What is often referred to in the literature as "the Selberg trace formula" is actually a particular case of the general formula Selberg proves in this paper.

The general formula he develops in section 2 applies to a Riemannian manifold S of any dimension, together with a locally compact group of isometries G acting on S, and a discrete subgroup of G.

In section 3, he treats the special case where S is the hyperbolic plane. G and its subgroup are chosen appropriately so that the formula relates to compact Riemannian surfaces (which are well-known to be expressible as quotients of the hyperbolic plane).

This is the formula as given on p.74 of Selberg's paper:

The left-hand side is effectively a sum over the Laplacian spectrum (i.e. the harmonic frequencies) of the compact Riemannian surface. Both left and right hand sides can be understood as distributions, where h is the 'test-function' being acted on (g is just an integral transform of h).

The second and third terms of the right-hand side are sums over primitive conjugacy classes of isometries on the surface. The {R} refers to conjugacy classes of elliptic isometries, and {P} to conjugacy classes of hyperbolic isometries. Note that Hejhal's 1976 paper (mentioned above) presents a simpler version where there are no elliptic conjugacy classes.

The N{P} in the third term are crucial here. They are the norms of primitive conjugacy classes of hyperbolic isometries. Roughly speaking the norm measures the factor by which such an isometry 'dilates' the hyperbolic plane (which is the universal covering surface of the compact Riemann surface in question). These norms are closely related to the lengths of primitive geodesics on the surface and, in the setting of (quantum) chaos, the periods of primitive orbits in certain flows.

The resemblance between this formula and the Riemann-Weil explicit formula is such that the N{P} correspond to the prime numbers, and the r_i on the left-hand side (which are directly linked to the Laplacian spectrum of the surface) correspond to the nontrivial zeros of the Riemann zeta function. Consequently, the resemblance is a major source of support for the spectral interpretation of the Riemann zeta function. Put very simply, the spectral interpretation argues that "the nontrivial zeros of the Riemann zeta function are eigenvalues in some setting".

The following survey article explains in detail the relationship between the Selberg trace formula and the Riemann zeta function:

D. Hejhal, "The Selberg trace formula and the Riemann zeta function", Duke Mathematics Journal 43 (1976) 441-482.

Also highly relevant:

D. Goldfeld, "Explicit Formulae as Trace Formulae", from Number Theory, Trace Formulas and Discrete Groups (K.E. Aubert, E. Bombieri and D. Goldfeld, eds.) (Academic, 1989) 281-288

"In his epoch-making paper, Selberg developed a general trace formula for discrete subgroups of GL(2,R). The analogies with the explicit formulae of Weil (relating very general sums over primes with corresponding sums over the critical zeroes of the zeta-function) are quite striking and have been the subject of much speculation over the years.

It is the object of this note to show that Weil's explicit formula can in fact be interpreted as a trace formula on a suitable space. The simplest space we have been able to construct for this purpose, at present, is the semidirect product of the ideles of norm one with the adeles, factored by the discrete subgroup Q* |X Q, the semidirect product of the multiplicative group of rational numbers with the additive group of rational numbers. We will show that for a suitable kernel function on this space, the conjugacy class side of the Selberg trace formula, is precisely the sum over the primes occurring in Weil's explicit formula.

This implies that the sum of the eigenvalues of the self-adjoint integral operator associated to the aforementioned kernel function is precisely the sum over the critical zeroes of the Riemann zeta-function occurring on the other side of Weil's formula. The relation between the eigenvalues of this integral operator and the zeroes of the zeta-function appears quite mysterious at present. What is lacking is a suitable generalization of the Selberg transform in this situation.

Finally, we should point out that our approach leads to various new equivalences to the Riemann Hypothesis, such as certain positivity hypotheses for the integral operators. Although we have worked over Q, for simplicity of exposition, it is not hard to generalize our relults to L-functions of arbitrary number fields."

Andy Sinton of UC Berkeley recently informed me (December 2003):

"Jay Jorgenson and Serge Lang are near completion on results that obtain the functional equation of Selberg zeta (or it's logarithmic derivative), they're also working on SL(2,C) as a Poisson summation despite Iwaniec's claim that "the functional equation...resists any decent interpretation as a kind of Poisson summation principle". Lang is teaching about it at Yale and there should be some lecture notes available sometime in the coming year."

Dan Bump suggests the following:

Iwaniec, H., Introduction to the Spectral Theory of Automorphic Forms, 2^nd edition, Graduate Studies in Mathematics 53 (AMS, 2002)

Chapter 10 covers the Trace Formula, and on p.154 we find a helpful note about Selberg zeta functions:

"If you will, the Selberg zeta-function satisfies an analogue of the Riemann hypothesis. However, the analogy with the Riemann zeta-function is superficial. First of all, the Selberg zeta function has no natural development into Dirichlet series. Furthermore, the functional equation...resists any decent interpretation as a kind of Poisson summation principle. Nevertheless, modern studies of Z(s) have caused a lot of excitement in mathematical physics (see [Sa1]). At least, one may say that the dream of Hilbert and Pólya of connecting the zeros of a zeta-function with eigenvalues of a self-adjoint operator is a reality in the context of Z(s)."

[Sa1] P. Sarnak, "Determinants of Laplacians", Communications in Mathematical Physics 110 (1987) 113-120.
 

Venkov, A., Spectral Theory of Automorphic Functions and its Applications, Mathematics and its Applications (Soviet Series), 51 (Kluwer, 1990)

Tamagawa, T., "On Selberg's trace formula", J. Fac. Sci. Univ. Tokyo Sect. I 8 (1960) 363-386

Hejhal, D., The Selberg Trace Formula for PSL(2,R), Volume I (Springer Lecture Notes 548, 1976)

"The Tamagawa paper is important because it is the origin of the representation theoretic approach to the trace formula."

Bump's 2001 lecture notes "Spectral Theory of SL(2,R)" include a proof of the Selberg trace formula.

See also:

J. Arthur "The Trace Formula and Hecke Operators", from Number Theory, Trace Formulas and Discrete Groups (K.E. Aubert, E. Bombieri and D. Goldfeld, eds.) (Academic, 1989)

"This lecture is intended as a general introduction to the trace formula. We shall describe a formula that is a natural generalization of the Selberg trace formula for compact quotient. Selberg also established trace formulas for noncompact quotients of rank 1, and our formula can be regarded as an analogue for general rank of these. As an application, we shall look at the 'finite case' of the trace formula. We shall describe a finite closed formula for the traces of Hecke operators on certain eigenspaces."

Andrew Bennett's very helpful applets for exploring the hyperbolic plane

A. Juhl's history of generalisations of Selberg zeta functions

D. Hejhal, "The Selberg trace formula for congruence subgroups", Bulletin of the AMS 81 (1975) 752-755.

C. Grosche, "Selberg supertrace formula for super Riemann surfaces III: bordered super Riemann surfaces", Commun. Math. Phys. 162 (1994) 591-632

"The analytic properties of the Selberg super zeta-functions on bordered super Riemann surfaces are discussed, and super-determinants of Dirac-Laplace operators on bordered super Riemann surfaces are calculated in terms of Selberg super zeta-functions." 
 

U. Bunke and M. Olbrich, "Group cohomology and the singularities of the Selberg zeta function associated to a Kleinian group", Annals of Mathematics 149 no.2 (1999) 627-689

[abstract:] "We prove Patterson's conjecture about the singularities of the Selberg zeta function associated to a convex-cocompact, torsion free group acting on a hyperbolic space."

U. Bunke and M. Olbrich, "Gamma cohomology and the Selberg zeta function" (preprint 11/94)

[abstract:] "We propose a new method for studying $n$- and $\Gamma$-cohomology of globalizations of Harish-Chandra modules, where $G=KAN$ is a rank one semisimple Lie group, $\Gamma$ is a discrete subgroup of $G$ and $n=Lie(N)$. We prove a conjecture of Patterson relating the singularities of Selberg zeta functions with the $\Gamma$-cohomology of principal series representations if $\Gamma$ is cocompact and torsion free."
 

P. Perry, "Resonances, zeta functions, and trace formulas for Kleinian groups" (preprint? Note: this PDF contains an irregularity in that the last first page appears as last page.)

P. Perry and S. Patterson, "The divisor of Selberg's zeta function for Kleinian groups", Duke Math. J. 106 No.2 (2001)

[summary by Peter G. Gilkay:] "Selberg's zeta-function is defined in terms of the length spectrum of a compact or, more generally, a finite volume hyperbolic surface. Its divisor is determined by the eigenvalues and scattering poles of the Laplacian and the Euler characteristic of the surface. The authors note "this relationship may be regarded as one form of Selberg's trace formula for a compact or finite volume surface and as a particularly precise quantization of an ergodic system, namely, the geodesic flow".

The authors extend this relationship to convex cocompact hyperbolic manifolds in all dimensions. They show the divisor of the Selberg zeta-function is determined by the eigenvalues and scattering poles of the Laplacian together with the Euler characteristic of the corresponding compactified manifold with boundary. In even dimensions, this uses work of Bunke and Olbrich.

The contents of the paper are as follows: 1. Introduction. 2. Symbolic dynamics and Selberg's zeta-function. 3. Geometry at infinity (coordinate neighborhoods, envelopes of horospheres, normal flow). 4. Review of scattering theory (model space, resolvant, eigenfunctions, operator). 5. The 'logarithmic derivative' of the scattering operator. 6. The logarithmic derivative of the zeta-function. 7. Computation of the divisor (spectral term, topological term, residues in odd and even dimensions).
Appendix A: An asymptotic volume formula for convex cocompact hyperbolic manifolds (by C. Epstein).
Appendix B: The scattering operator and zeta-function for a class of cylindrical manifolds."
 

E. Bogomolny, "Quantum and arithmetical chaos" (preprint 12/03, based on lectures given at Les Houches School "Frontiers in Number Theory, Physics and Geometry", March 2003)

[abstract:] "The lectures are centered around three selected topics of quantum chaos: the Selberg trace formula, the two-point spectral correlation functions of Riemann zeta function zeros, and of the Laplace-Beltrami operator for the modular group. The lectures cover a wide range of quantum chaos applications and can serve as a non-formal introduction to mathematical methods of quantum chaos."
 

D. Mayer, "The thermodynamic formalism approach to Selberg's zeta function for PSL(2,Z)", Bulletin of the AMS 25 (1991) 55-60. 

"The thermodynamic formalism...leads to a rather explicit representation of the Smale-Ruelle function and hence also of the Selberg function for PSL(2,Z) in terms of Fredholm determinants of transfer operators of the map T_G. Finally, combining our results with classical ones for the Selberg function derived from the trace formula suggests also a seemingly new formulation of Riemann's hypothesis on his zeta function in terms of the transfer operators of T_G."

Cheng-Hung Chang and D. Mayer, "The transfer operator to Selberg's zeta function and modular Maass waveforms for PSL(2,Z)", from Emerging Applications of Number Theory (Mathematics and its Applications vol. 109, eds. D. Hejhal, M. Gutzwiller, et. al.) (Springer, 1999)

Cheng-Hung Chang and D. Mayer, "Thermodynamic formalism and Selberg's zeta function for modular groups", Regular and Chaotic Dynamics 5 no.3 (2000) 281-312

Cheng-Hung Chang and D. Mayer, "Eigenfunctions of the transfer operators and period functions for modular groups", from Dynamical, Spectral, and Arithmetic Zeta Functions (San Antonio, TX, 1999), (Contemporary Mathematics 290) (AMS, 2001) 1-40

A. Momeni and A. Venkov, "Mayer transfer operator approach to Selberg zeta function" (preprint 08/2010)

[abstract:] "These notes are based on three lectures given by second author at Copenhagen University (October 2009) and at Aarhus University, Denmark (December 2009). We mostly present here a survey of results of Dieter Mayer on relations between Selberg and Smale-Ruelle dynamical zeta functions. In a special situation the dynamical zeta function is defined for a geodesic flow on a hyperbolic plane quotient by an arithmetic cofinite discrete group. More precisely, the flow is defined for the corresponding unit tangent bundle. It turns out that the Selberg zeta function for this group can be expressed in terms of a Fredholm determinant of a classical transfer operator of the flow. The transfer operator is defined in a certain space of holomorphic functions and its matrix representation in a natural basis is given in terms of the Riemann zeta function."
 

D. Zagier and J. Lewis, "Period functions and the Selberg zeta function of the modular group", from The Mathematical Beauty of Physics, Adv. Series in Math. Physics 24 (World Scientic, 1997) 83-97
 

A. Terras and D. Wallace, "Selberg's trace formula on the k-regular tree and applications", ,i>Int. J. of Math. and Math. Sci. 8 (2003) 501-526.
 

J.S. Friedman, "The Selberg trace formula and Selberg zeta-function for cofinite Kleinian groups with finite-dimensional unitary representations" (preprint 10/04)

[abstract:] "For cofinite Kleinian groups, with finite-dimensional unitary representations, we derive the Selberg trace formula. As an application we define the corresponding Selberg zeta-function and compute its divisor, thus generalizing results of Elstrodt, Grunewald and Mennicke to non-trivial unitary representations. We show that the presence of cuspidal elliptic elements sometimes adds ramification point to the zeta function. In fact, if D is the ring of Eisenstein integers, then the Selberg zeta-function of PSL(2,D) contains ramification points and is the sixth-root of a meromorphic function."
 

J. Fiala and P. Kleban, "Generalized number theoretic spin chain-connections to dynamical systems and expectation values", J. of Stat. Physics 121 (2005) 553-577

[abstract:] "We generalize the number theoretic spin chain, a one-dimensional statistical model based on the Farey fractions, by introducing a new parameter x > 0. This allows us to write recursion relations in the length of the chain. These relations are closely related to the Lewis three-term equation, which is useful in the study of the Selberg zeta-function. We then make use of these relations and spin orientation transformations. We find a simple connection with the transfer operator of a model of intermittency in dynamical systems. In addition, we are able to calculate certain spin expectation values explicitly in terms of the free energy or correlation length. Some of these expectation values appear to be directly connected with the mechanism of the phase transition."
 

N. Kurokawa and M. Wakayama, "Casimir effects on Riemann surfaces", Indagationes Mathematicae 13 (1) (2002) 63–75

[abstract:] "The Casimir effect whose existence was first predicted by Casimir in 1948 is considered as a manifestation of macroscopic quantum field theory. This force is evaluated theoretically by using the value of the Riemann zeta function at -3. The aim of the present paper is to introduce a similar Casimir energy for a Riemann surface, and to express it by a special value of the Mellin transform of a theta series arising from the heat kernel and also by a weighted integral of the logarithm of the Selberg zeta function."
 

S. Egger né Endres and F. Steiner, "An exact trace formula and zeta functions for an infinite quantum graph with a non-standard Weyl asymptotics" (preprint 04/2011)

[abstract:] "We study a quantum Hamiltonian that is given by the (negative) Laplacian and an infinite chain of $\delta$-like potentials with strength $\kappa>0$ on the half line $\rz_{\geq0}$ and which is equivalent to a one-parameter family of Laplacians on an infinite metric graph. This graph consists of an infinite chain of edges with the metric structure defined by assigning an interval $I_n=[0,l_n]$, $n\in\nz$, to each edge with length $l_n=\frac{\pi}{n}$. We show that the one-parameter family of quantum graphs possesses a purely discrete and strictly positive spectrum for each $\kappa>0$ and prove that the Dirichlet Laplacian is the limit of the one-parameter family in the strong resolvent sense. The spectrum of the resulting Dirichlet quantum graph is also purely discrete. The eigenvalues are given by $\lambda_n=n^2$, $n\in\nz$, with multiplicities $d(n)$, where $d(n)$ denotes the divisor function. We thus can relate the spectral problem of this infinite quantum graph to Dirichlet's famous divisor problem and infer the non-standard Weyl asymptotics $\mathcal{N}(\lambda)=\frac{\sqrt{\lambda}}{2}\ln\lambda +\Or(\sqrt{\lambda})$ for the eigenvalue counting function. Based on an exact trace formula, the Vorono\"i summation formula, we derive explicit formulae for the trace of the wave group, the heat kernel, the resolvent and for various spectral zeta functions. These results enable us to establish a well-defined (renormalized) secular equation and a Selberg-like zeta function defined in terms of the classical periodic orbits of the graph, for which we derive an exact functional equation and prove that the analogue of the Riemann hypothesis is true."
 

P.A. Perry and F.L. Williams, "Selberg zeta function and trace formula for the BTZ black hole" (preprint 02/03)

[abstract:] "A Selberg zeta function is attached to the three-dimensional BTZ black hole, and a trace formula is developed for a general class of test functions. The trace formula differs from those of more standard use in physics in that the black hole has a fundamental domain of infinite hyperbolic volume. Various thermodynamic quantities associated with the black hole are conveniently expressed in terms of the zeta function."
 

M. Nardelli, "On some mathematical connections concerning the three-dimensional pure quantum gravity with negative cosmological constant, the Selberg zeta-function, the ten-dimensional anomaly cancellations, the vanishing of cosmological constant, and some sectors of string theory and number theory" (preprint 06/2008)

[abstract:] "This paper is a review of some interesting results that has been obtained in the study of the quantum gravity partition functions in three-dimensions, in the Selberg zeta function, in the vanishing of cosmological constant and in the ten-dimensional anomaly cancellations. In the Section 1, we have described some equations concerning the pure three-dimensional quantum gravity with a negative cosmological constant and the pure three-dimensional supergravity partition functions. In the Section 2, we have described some equations concerning the Selberg super-trace formula for Super-Riemann surfaces, some analytic properties of Selberg super zeta-functions and multiloop contributions for the fermionic strings. In the Section 3, we have described some equations concerning the ten-dimensional anomaly cancellations and the vanishing of cosmological constant. In the Section 4, we have described some equations concerning p-adic strings, p-adic and adelic zeta functions and zeta strings. In conclusion, in the Section 5, we have described the possible and very interesting mathematical connections obtained between some equations regarding the various sections and some sectors of number t heory (Riemann zeta functions, Ramanujan modular equations, etc…) and some interesting mathematical applications concerning the Selberg super-zeta functions and some equations regarding the Section 1."

M. Nardelli, "On the physical interpretation of the Riemann zeta function, the Rigid Surface Operators in Gauge Theory, the adeles and ideles groups applied to various formulae regarding the Riemann zeta function and the Selberg trace formula, p-adic strings, zeta strings and p-adic cosmology and mathematical connections with some sectors of String Theory and Number Theory" (preprint 10/2008)

[abstract:] "This paper is a review of some interesting results that has been obtained in the study of the physical interpretation of the Riemann zeta function as a FZZT Brane Partition Function associated with a matrix/gravity correspondence and some aspects of the Rigid Surface Operators in Gauge Theory. Furthermore, we describe the mathematical connections with some sectors of String Theory (p-adic and adelic strings, p-adic cosmology) and Number Theory.

In the Section 1 we have described various mathematical aspects of the Riemann Hypothesis, matrix/gravity correspondence and master matrix for FZZT brane partition functions. In the Section 2, we have described some mathematical aspects of the rigid surface operators in gauge theory and some mathematical connections with various sectors of Number Theory, principally with the Ramanujan's modular equations (thence, prime numbers, prime natural numbers, Fibonacci's numbers, partitions of numbers, Euler’s functions, etc...) and various numbers and equations related to the Lie Groups. In the Section 3, we have described some very recent mathematical results concerning the adeles and ideles groups applied to various formulae regarding the Riemann zeta function and the Selberg trace formula (connected with the Selberg zeta function), hence, we have obtained some new connections applying these results to the adelic strings and zeta strings. In the Section 4 we have described some equations concerning p-adic strings, p-adic and adelic zeta functions, zeta strings and p-adic cosmology (with regard the p-adic cosmology, some equations concerning a general class of cosmological models driven by a nonlocal scalar field inspired by string field theories). In conclusion, in the Section 5, we have showed various and interesting mathematical connections between some equations concerning the Section 1, 3 and 4."
 

D. Fried, "The zeta functions of Ruelle and Selberg. I.", Ann. Sci. Ecole Norm. Sup. (4) 19 (1986), 491-517.
 

A. Venkov and A. Nikitin, "Selberg trace formula, Ramanujan graphs and some problems of mathematical physics", Algebra Anal. 5 (1993) 1-76.
 

E. d'Hoker and D. Phong, "Multiloop amplitudes for the bosonic Polyakov string", Nuclear Physics B 269 (1986) 205-234.
 

N. Balazs and A. Voros, "Chaos on the pseudosphere", Physics Reports 143 (1986) 109-240.

A. Voros, "Spectral functions, special functions and the Selberg zeta function", Communications in Mathematical Physics 110 (1987) 439-465.
 

D. Wallace, "The Selberg trace formula for SL(3,Z)\ SL(3,R)/ SO(3,R)", Transanctions of the AMS (new series) 345 (1994), 136.
 

H. Ninnemann, "Gutzwiller's octagon and the triangular billiard T*(2,3,8) as models for the quantization of chaotic systems by Selberg's trace formula", PhD Thesis, Universität Hamburg (1994) also International Journal of Modern Physics B 9 (1995) 1647.

M. Duflo and J.P. LaBesse, "Sur la formule des traces de Selberg", Ann. Ecole Norm. Sup. [IV] 4 (1971) 193-284.

F.I. Mautner, "Sur certaines analogues des formules de Riemann-von Mangoldt-Selberg-Weil", C.R. Acad. Sci. Paris 279 (1974) 851-853.

J. Arthur, "The Selberg trace formula for groups of F-rank one", Annals of Mathematics 100 (1974) 326-385.

N. Subia, "Formule de Selberg et formes d'espaces hyperboliques compactes", Springer Lecture Notes 497 (1975) 674-700.

R. Gangolli, "Zeta functions of Selberg's type for compact space forms of symmetric spaces of rank one", Illinois Journal of Mathematics 21 (1977) 141.

A. Voros, "Spectral functions, special functions, and the Selberg zeta function", Communications in Mathematical Physics 110 (1987) 439-465.

A. Venkov, "Spectral theory of automorphic functions, the Selberg zeta function, and some problems of analytic number theory and mathematical physics", Russian Math. Surveys (3) 34 (1979).

V. Baladi, "Periodic orbits and dynamical spectra", Ergod. Th. and Dynam. Sys. 18 (1968) 255-292

D. Barbasch and H. Moscovici, "L²-index and the Selberg trace formula", Journal of Functional Analysis 53 (2) (1983) 151-201.

A. Beilinson and J. Manin, "The value of the Selberg zeta function at integral point", Funct. Anal. Appl. 21 (1987) 58-60.

U. Bröcker, "On Selberg's zeta functions, topological zeros and determinant formulas", Technical report SFB 288 (1994)

U. Bunke and M. Olbrich (appendix by A. Juhl), "The wave kernel for the Laplacian on classical locally symmetric spaces of rank one, theta functions, trace formulas and the Selberg zeta function", Ann. Glob. Anal. Geom. 12 (1994) 357-405.

U. Bunke and M. Olbrich, "Gamma-cohomology and the Selberg zeta function", J. Reine Angew. Math. 467 (1995) 199-219.

U. Bunke and M. Olbrich, Selberg Zeta and Theta Functions. A differential operator approach, vol. 83 of Mathematical Research (Akademie-Verlag, 1995).

U. Bunke and M. Olbrich, "Group cohomology and the singularities of the Selberg zeta function associated to a Kleinian group", Ann. of Math. 149 (2) (1999) 627-689.

P. Cartier and A. Voros, "Une nouvelle interprétation de la formule des traces de Selberg", In The Grothendieck Festschrift, volume 87 of Progress in Mathematics (Birkhäuser, 1990) 1-67.

A. Deitmar, "A determinant formula for the generalized Selberg zeta function", Quart. J. Math. Oxford 47 (2) (1996) 435-453.

J. Elstrodt, "Die Selbergsche Spurformel f¨r kompakte Riemannsche Flächen", Jahresber. Deutsch. Math.-Verein., 83 (1981) 45-77.

J. Elstrodt, F. Grunewald and J. Mennicke, Groups Acting on Hyperbolic Space: Harmonic Analysis and Number Theory (Springer-Verlag, 1988)

J. Fischer, An approach to the Selberg trace formula via the Selberg zeta function volume 1283 of Lecture Notes in Mathematics (Springer, 1987)

S.V. Fomin and I.M. Gelfand, "Geodesic flow on manifolds of constant negative curvature", Uspekhi Mat. Nauk 7 (1952) 118-137

D. Fried, "The zeta functions of Ruelle and Selberg, I", Ann. Sci. École Norm. Sup. 19 (1986) 491-517.

R. Gangolli and G. Warner, "On Selberg's trace formula", J. Math. Soc. Japan 27 (1975) 328-343

Y. Gon, "Gamma factors for generalized Selberg zeta functions," Proceedings of Japan Academy 7 (7) (1995) 148-150

Y. Gon, "Gamma factors of Selberg zeta functions and functional equation of Ruelle zeta functons", Math. Ann. 308 (1997) 251-278

M.C. Gutzwiller, "Physics and Selberg's trace formula", Contemp. Math. 53 (1986) 215-251.

M. Hirano, "On theta type functions associated with the zeros of the Selberg zeta functions", Manuscripta Math. 92 (1997) 87-105.

E. Hopf, "Ergodic theory and the geodesic flow on surfaces of constant negative curvature", Bull. Amer. Math. Soc. 77 (1971) 863-877.

A. Juhl, "Zeta-Funktionen, Index-Theorie und hyperbolische Dynamik", Habilitationsschrift, Humboldt-Universität Berlin, 1993

S. Koyama, "Determinant expression of Selberg zeta functions I", Trans. Amer. Math. Soc. 324 (1991) 149-168.

N. Kurokawa, "Multiple sine functions and Selberg zeta functions", Proc. Japan. Acad. Ser. A Math. Sci. 67 (1991) 61-64

J. Lewis and D. Zagier, "Period functions and the Selberg zeta function for the modular group", Technical Report 112, Max-Planck-Institut, 1996

L.B. Parnovski, "The Selberg zeta function for cocompact discrete subgroups of $SO^{+}(1,\nu)$, Funkt. Anal. I. Pril. 26 (1992) 55-64 (in Russian)

S.J. Patterson, "The Selberg zeta-function of a Kleinian group", In Number Theory, Trace Formulas and Discrete Groups: Symposium in honor of Atle Selberg, Oslo, Norway (1987) 409-441.

P. Perry, "The Selberg zeta function and a local trace formula for Kleinian groups", J. Reine Angew. Math. 410 (1990) 116-152.

P. Perry, "The Selberg zeta function and scattering poles for Kleinian groups", Bull. Amer. Math. Soc. 24 (1991) 327-333.

A. Rocha, "Meromorphic extesion of the Selberg zeta function for Kleinian groups via thermodynamical formalism", Math. Proc. Cambridge Phil. Soc. 119 (1996) 179-190

H. Rugh, "Generalized Fredholm determinants and Selberg zeta functions for Axiom A dynamical systems", Ergodic Theory and Dynamical Systems 16 (1996) 805-819.

R. Schuster, "Spectral estimates for compact hyperbolic space forms and the Selberg zeta functions for p-spectra, I", Z. Anal. Anwendungen, 11 (1992) 343-358

A.B. Venkov, "Spectral theory of automorphic functions, the Selberg zeta function, and some problems of analytic number theory and mathematical physics", Russian Math. Surveys 34 (1979) 79-153

M.-F. Vigneras, "L'equation fonctionelle de la fonction zêta de Selberg du groupe modulaire PSL(2,Z)", Astérisque 61 (1979) 235-249.

M. Wakayama, "Zeta functions of Selberg's type associated with homogenous vector bundles", Hiroshima Math. J. 15 (1985) 235-295.

M. Wakayama, "Zeta functions of Selberg's type for non-compact quotient of SU(n,1) (n >2)", Hiroshima Math. J. 14 (1985) 597-618.

M. Wakayama, "A formula for the logarithmic derivative of Selberg's zeta function", J. Math. Soc. Japan 41 (1989) 436-471.

M. Wakayama, "A note on the Selberg zeta function for compact quotients of hyperbolic spaces", Hiroshima Math. J. 21 (1991) 539-555

N.R. Wallach, "On the Selberg trace formula in the case of a compact quotient", Bull. Amer. Math. Soc. 82 (1976) 171-195

G. Warner, "Selberg's trace formula for nonuniform lattices: The R-rank one case", volume 6 of Advances in Math. Supp. Studies (Academic, 1979) 1-142.

F.L. Williams, "A factorization of the Selberg zeta function attached to rank I space forms", Manuskripta Math. 77 (1992) 17-39.

a directory of all known zeta functions

---

books

---

A. Selberg, Collected Papers, Vol. I (Springer-Verlag, 1989)

I.M. Gelfand, M.I. Graev and I.I. Piatetskii-Shapiro, Representation Theory and Automorphic Functions (Saunders, 1969)

I. Chavel, Eigenvalues in Riemannian Geometry (Academic Press, 1984)

Iwaniec, H., Introduction to the Spectral Theory of Automorphic Forms, 2^nd edition, Graduate Studies in Mathematics 53 (AMS, 2002)

M. Scott Osborne and G. Warner, Selberg Trace Formula III : Inner Product Formulae (Initial Considerations) (AMS, 1983)

K. Aubert, E. Bombieri and D. Goldfeld (editors), Number Theory, Trace Formulas, and Discrete Groups: Symposium in Honor of Atle Selberg, Oslo, Norway, July 14-21, 1987 (Academic Press, 1989)

J. Fischer (Editor), An Approach to the Selberg Trace Formula Via the Selberg Zeta-Function (Lecture Notes in Mathematics 1253) (Springer-Verlag, 1987)

D. Hejhal, The Selberg Trace Formula for PSL(2,R), Volume I and II (Springer, 1976 & 1983)

U. Bunke, M. Olbrich, Selberg Zeta and Theta Functions: A Differential Operator Approach (Wiley, 1995)

"Employs a version of the Selberg trace formula to illuminate the connection between the spectrum of certain elliptical differential operators, and the theory of zeta and theta functions for bundles on compact locally symmetric spaces and rank one. Also describes the theta function of Riemannian surfaces with cusps, and alternative descriptions of the singularities of the Selberg zeta functions in terms of Lie algebra and group cohomology. Includes explicit worked examples."

U. Christian, Selberg's Zeta-, L-, and Eisenstein Series (Springer, 1983)

C. Grosche, Path Integrals, Hyperbolic Spaces, and Selberg Trace Formulae (World Scientific, 1996)

"In this volume, a comprehensive review is given for path integration in two- and three-dimensional homogeneous spaces of constant curvature, including an enumeration of all coordinate systems which allow separation of variables in the Hamiltonian and in the path integral. The corresponding path integral solutions are presented as a tabulation. In addition, an overview is presented on some recent achievements in the theory of the Selberg trace formula on Riemann surfaces, its super generalization, and their use in mathematical physics and quantum chaos. The volume also contains results on the study of the properties of a particular integrable billiard system in the hyperbolic plane, a proposal concerning interbasis expansions for spheroidal coordinate systems in four-dimensional Euclidean space, and some further results derived from the Selberg (super-) trace formula."

Steven Zelditch, Selberg Trace Formulae and Equidistribution Theorems for Closed Geodesics and Laplace Eigenfunctions: Finite Area Surfaces (Memoirs of the AMS 465) (AMS, 1992)

A. Juhl, Cohomological Theory of Dynamical Zeta Functions (Progress in Mathematics 194) (Birkhauser, 2001)