, 
and 
. 2-D spirals at these parameter values are stationary (not meandering),
and 3-D scrolls have negative but relatively small filament tension. In
different experiments, we kept the parameters fixed and varied only size
of the medium. We used explicit Euler (first-order forward time) differencing,
with the simplest 7-point approximation of the 3-D Laplacian operator.
Time step (t.s.) was fixed to be 0.03 time units (t.u.), i.e. math
units of time of Eq. (2), and space step (s.s.)
was fixed to be 0.5 space units (s.u.).
If the size of the medium is just large enough to contain the scroll
wave but too small to let the filament instability to evolve, then the
simple scroll wave persists, purely independent on one of the spatial variables.
Fig. 2 shows such a scroll wave in the
medium 
s.s. large. Its straight form is stabilised by its short length and also
by interaction with boundary, the farther one in the figure. Due to this
interaction, the rotation is not rigid but modulated by a rather slow motion,
as it is seen in Fig. 5 below, the drift
along the boundary. As this solution does not depend on the vertical coordinate,
it is the well known purely 2-D phenomenon, described by Ermakova &
Pertsov [1986].
Increasing the size of the medium just by one space step in each direction,
up to 
s.s., makes the simple scroll wave unstable. Its intermediate evolution
involves curving the filament, touching the boundaries and annihilation
of a piece of it, leading to its doubling, which eventually leads to the
pattern shown in Fig. 3.
Figure 3: Double scroll wave, in the medium of
s.s. large. Notations are the same as in Fig. 2.
The two filaments exhibit irregular dynamics but always remain only two,
i.e. do not split, annihilate or join.
It is a double scroll, in each orthogonal cross-section looking as a pair of likewise rotating spirals, or a two-armed spiral. This rotation is by no means stationary, and is clearly different in different cross-sections. The evolution looks like a competition between inherent instability of shape of each filament, and their stabilisation by mutual attraction. This attraction is, apparently, of the same nature as that observed in 2-D experiments by Ermakova et al. [1989]. Its dynamics are apparently chaotic rather than biperiodic (see Fig. 5 below). However, after this double-scroll configuration has been reached, the dynamics are only curving of the two filaments, but not multiplications or annihilations.
Further increase in medium size makes any persistent structures unstable
very soon, and dynamics become highly complicated and visually disordered.
Figure 4 shows two snapshots of wavefronts
in a medium 
s.s. large, made at different time moments. One of the snapshots shows
four vortex filaments, another shows six; in general, their number `oscillates'
between two and seven. Careful visual analysis of `movie' of pictures like
Fig. 4 shows relatively long-living (actually,
just a few rotations) structures like pairs of twisted helicoidal filaments;
one of them can be seen in Fig. 4(a).
This is, however, just a visual observation, and has not been tested by
any objective method.
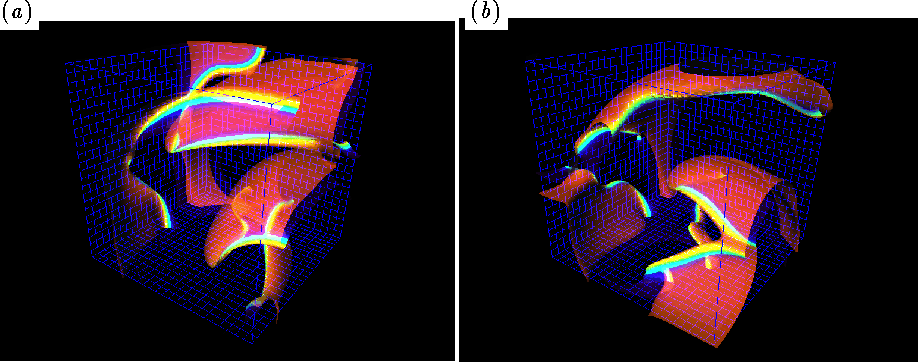
Figure 4: Multiple scroll waves, in the medium of
s.s. large. Notations are the same as in Fig. 2.
(a) 4 filaments can be seen. (b) 2460 t.s. (73.8 t.u. or
about two periods) later, 6 filaments can be seen.
Scalar time series were recorded for all the three cases illustrated
above; the Fourier spectra of the series are shown in Fig. 5.
There is a clear distinction in spectra of the nearly periodic activity
in the
medium and apparently chaotic one in bigger media. It is interesting, however,
that spectra of
and
media look similar, despite the evolution of the filaments is drastically
different. This shows that the scalar time series are not an adequate tool
for analysis of this complex spatio-temporal activity. Attempts to estimate
correlation dimension of the attractors in
and
media with the method of Rosenstein et al. [1993]
showed no saturation in embedding dimensions of up to 9.
Figure 5: Magnitude spectra of time series recorded in
the numerics illustrated by Figs 2-4,
respectively. Time series were 8192 values of 
over a half of the medium, recorded in every 10 t.s.=0.3 t.u. The horizontal
scale in all three graphs is 1024 harmonics, which corresponds to 4.17
t.u. 
. Spectrum (a) shows nearly periodic dynamics; higher harmonics
are slightly split due to the slow motion of the scroll along the boundary.
Spectra (b,c) are qualitatively the same and show irregular dynamics,
with the main peak corresponding to the rotating frequency. The main frequency
in (b,c) is different from that of (a); this reveals strong
interaction of vortices with each other and hence inapplicability of the
asymptotic theory.
Low-dimensional chaotic attractors may be possible in smaller media. However, as example of Fig. 2 shows, such an attractor would not be the only one in the system, and so studying it will require choice of appropriate initial conditions, which we failed to find so far. Perhaps, double scroll would be a helpful heuristics here.