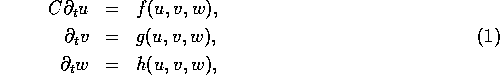
Biophysical membrane excitation equations are of the form:
where u=u(t) is the transmembrane voltage, C is specific membrane capacitance, f is transmembrane current density, vector v=v(t) describes the fast gating variables, and vector w=w(t) comprises slow gating variables and intra- and extra-cellular ionic concentrations, and g and h describe their kinetics. The variables u and v have comparable characteristic times.
We begin with a bidomain approach, for a single isolated cell with an
intracellular domain , 
, external domain, 
, and the
membrane surface, 
, and introduce the electrostatic potential
and 
in and , 
and 
as
limit values of and at , and electric charge
densities 
and 
at the inside and outside surface of the membrane.
1) Intracellularly, electroneutrality of the cytoplasm means for 
,
for a scalar specific conductivity 
.
2) In the extracellular domain, electroneutrality means for 
:
and for a homogeneous external field,
In the case of a tissue of cells, Eq. (4) is to be replaced -
e.g. for cells in a regular 3-dimensional grid, the domain 
forms the elementary volume of the grid, and (4) is to
be replaced by periodic boundary conditions for the ``own'' cell potential
or the ``oscillatory component'' of the potential, in terminology of Plonsey & Barr [1986] and Krassowska et al. [1990].
3) In the membrane, the boundary conditions of the ``volume equations''
(2,3) for 
:
and surface balance of charges on the interior and exterior sides of the membrane;
here f, is the transmembrane current, 
are specific
conductivities, and 
is the Laplacian operator on the membrane
surface. For simplicity of notations, we assume here that
are constant. Electroneutrality of a membrane element gives
The membrane capacitance is
and transmembrane voltage is
After defining 
, through local values of
u, v and w, and local kinetic equations for v and w from
(1), these equation form a closed system, which determines
evolution of the distribution of electric properties over the cell at given
, and so describe the action of the external electric field onto
the cell.
