Following the ideas of Krassowska and Neu [1994] we will now simplify this extensive nonlinear system of partial differential equations; note that in the electric part of the equations, all the nonlinearity is located in the term f(), and the remaining linear problem can be (in principle) solved. Summing the Eqs. (7) and (8), we get a linear equation
for the overall current balance of the membrane element, which, together with the equations
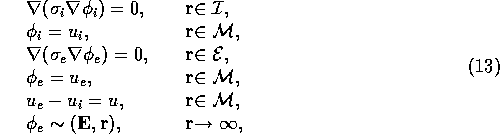
constitute a well posed elliptic problem for finding 
and
at given 
and u. Differentiation of
(10) by time and substituting into (7) or
(8), together with the slow equations, yields then the
resulting system of equations of the form
where u, v and w are now functions of time and position on the
membrane, 
is a linear (generally, integro-differential) operator in
a space of scalar functions on the membrane, and 
is a linear
operator mapping vectors to scalar functions on the membrane. The
specific forms of and depend on the geometry of 
and on the coefficients 
and 
. We use the
following properties of these operators:
vanishes if u is spatially homogeneous over the membrane, over the membrane surface is zero for any u
, and
over the membrane surface is zero for
any .
These properties follow from the derivation of (14).
represents the currents between different loci of membrane, both through
interior and exterior domains, and is the additional current
due to the external field.
