Due to ergodicity of 
, averaging over time and in are
equivalent, and it is enough to proof the statements of the Theorem for
the -averaged squared distance:
which equals I(t,u) for almost all u with respect to .
Straightforward calculations give:
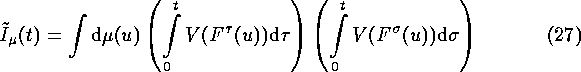
(definition of q(t)),
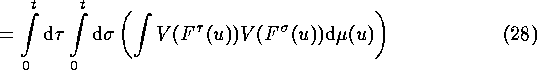
(change of order of integration)
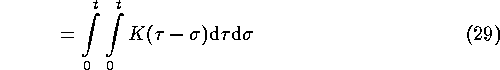
(definition of 
),
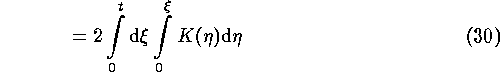
(change of independent variables, 
),
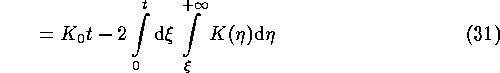
(definition of 
)
(convergence of ).
(L'Hospital's rule). The last estimation is the statement (9) of the Theorem.
Analogously, using (10) in (32) in addition to (7) leads to a more accurate estimation (11).
