Waves of propagating excitation are observed in active media of physical, chemical and biological origin [1, 2, 3, 4, 5]. The simplest solution to the underlying system of equations, usually of the reaction-diffusion type, is a solitary propagating pulse. Autowave media are characterised by all-or-none nature of these waves or at least a discrete spectrum of their amplitude and profile, as these parameters are determined by the balance between energy income and dissipation.
The first nontrivial two-dimensional generalisation of the solitary one-dimensional pulse, after the solitary plane wave, is a smoothly curved wave, which in every small domain looks like a solitary plane wave propagating in some direction. The local propagation velocity of such a wave differs from that of the corresponding plane wave for various reasons, the most important of which is the wave curvature. The dependence of wave velocity on its curvature (usually, in a linear approximation) delivers closed equations of motion of its front or crest line, which constitutes the essence of the kinematic approach [7, 10, 11]. The term `kinematic description' was introduced to stress the fact that all the underlying physics has been concentrated in a few phenomenological constants, defining the dependence of the velocity on the curvature, whereafter the prediction of the movement of the wave becomes a purely geometric problem in space-time. The curvature-velocity dependence can be obtained by singular perturbation techniques, starting from the solution of steadily propagating pulse [6, 7]. In some circumstances this may not be enough, as it is the case for the Kuramoto-Sivashinsky equation [7, 8], where inverse dependence of velocity on curvature requires account of higher derivatives of curvature along the wave.
A more complicated 2D pattern is a broken wave. The most important case
of such structures are rotating spiral waves of excitation, observed in
many autowave media [1, 2, 3, 4, 5], and are of
significant practical interest in cardiac muscle [9], where
they underlie dangerous pathologies like tachyarrhythmias and
fibrillation. If the waves are rare, so that next wave does not feel
the traces of the previous one that propagated through the same point,
and slightly curved, then the crest line of the wave can be defined,
which is now not a closed line or line ending on medium boundaries, but
has an end or `tip' inside the medium.
This line crosses a
region with the boundary, drawn by the tip. In this region, motion of
the crest line can be described by the kinematic equations. These
equations now require boundary conditions at the tip trajectory, and
some more conditions are required to determine the trajectory itself,
i.e. the movement of the tip. Both types of equations relate geometry
and motion of the crest line near the tip, and we shall call both wave
tip motion equations.
The `classical' kinematic approach, developed by Davydov, Mikhailov, Zykov et al. [10, 11], is based on the following main equations:
where the wave form is described in terms of time t and arclength s
measured from the wave tip, V(s,t) and G(s,t) are normal and
tangential components of wave velocity, K(s,t) is crest line
curvature, and subscript 0 refers to the value at the tip, i.e. at
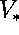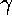s=0. Constants D, 
, 
and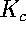 
are medium
parameters (more formal definitions will be given below).
Equation (1) is well known in many areas of physics, e.g. in flame propagation and crystal growth (see references in [13]), and for excitation pulses in reaction-diffusion systems it has been derived e.g. by Kuramoto [7]. Equation (2) has been first proposed from phenomenological considerations; in [10, 11] it has been substantiated by perturbation technique similar to that used by Kuramoto [7], starting from the solution in the form of a broken plane wave propagating steadily and in the direction orthogonal to itself, and neglecting, at some stage, the curvature variations along the wave. The last equation in this system, (3), is the weakest basis of the existing theory; as in [11], it is in fact an arbitrary suggestion introduced to close the system of equations. In the stationary case, equation (3) can be satisfied in two different ways; usually it was assumed that
These equations, together with definition of geometrical quantities involved, constitute a well posed `kinematic' problem, where all underlying physics is concentrated in a few coefficients. This theory and its generalization to curved surfaces, to inhomogeneous, refractory and nonstationary media and to three dimensions has been used to analyse the dynamics of spiral and scroll waves. A recent review of the results can be found in [11].
In this paper, we discard the simplification and arbitrary suggestion mentioned above, and derive the motion equations for the wave tip consistently by singular perturbation techniques using generic assumptions (Section 2). The resulting equations of the wave tip have proved more complicated and diverse than the traditional ones (2, 3). As an example, we apply the new equations to the problem of a stationary spiral wave (Section 3). In this simplest nontrivial problem, the traditional equations have proved to be a special case, giving a unique solution while, in general, there may be many, and different asymptotical magnitudes of certain characteristic quantities. The last section is devoted to the discussion of most interesting physical consequences and further directions.
