We consider a reaction-diffusion system in the plane,
where 
, 
is a column-vector of state variables,
describes local kinetics, 
is an
matrix of diffusion coefficients and 
is the
two-dimensional Laplacian operator. For a chemical excitable medium, u are
concentrations of reagents and 
reaction rates; for cardiac
muscle u are transmembrane voltage, ionic concentrations and gating
variables.
System (5) is obtained as a perturbation of a special system,
that belongs to Winfree's `rotor boundary' 
[15] in the
parametric space. Near this boundary, the rotation period and core
diameter of the spiral wave become very large, and we assume that at
the boundary, a stationary propagating broken wave solution 
exists. Denoting
normal (propagation) velocity by 
and sideward (`growth') velocity
by 
, this hypothetical solution can be defined as
The coordinate 
is chosen so that the broken wave is at
. The form (7) is the generic form of a stationary
propagating broken wave solution taking account of the translational
symmetry of the reaction-diffusion system. That it is not an arbitrary
two-dimensional solution breaking the translational symmetry, but
specifically the broken wave, is given by the requirements that
i.e. far from the tip, the broken wave 
becomes a plane
wave, with the profile of a solitary pulse 
propagating
through resting state 
. Then the perturbed system (5) also
has a plane wave solution,
with a profile 
and a velocity 
close to 
and .
We are interested in solutions of (5) in the form of the broken wave, slightly perturbed and smoothly curved. Let us introduce the coordinate system (s,q) related to the crest line (see Fig. 1a):
where 
is the crest line equation, 
is the unit
normal and s is the arclength measured from the tip.
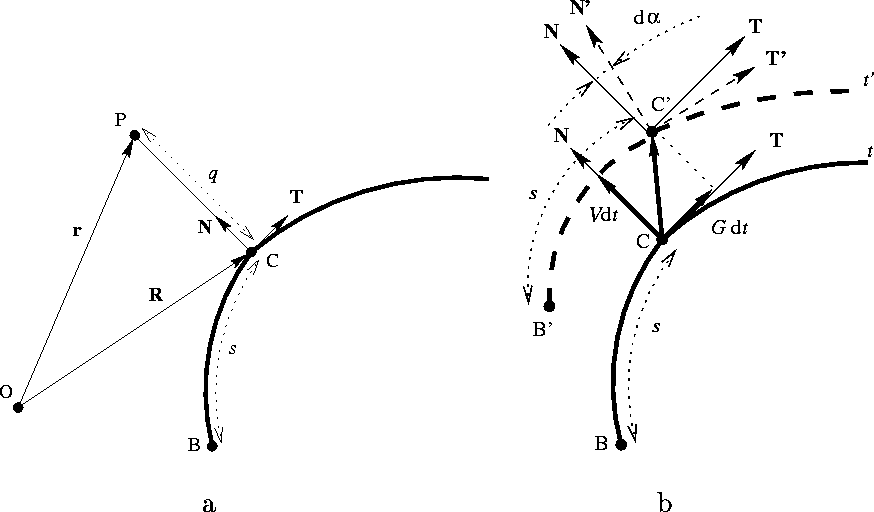
Figure 1:
Kinematic description of motion of the crest line.
a The curvilinear coordinates related to the crest line shown
by the bold line. O is the origin, B -- the wave break point (tip), C -- a point
on the crest-line at the distance s from the tip, 
-- its
radius-vector, 
and 
-- tangent and normal unit
vectors, P -- a point in the plane at the distance q from C in the
directin of , 
its radius-vector. Thus, s and q
are the curvilinear coordinates of the point P.
b Velocities related to the moving crest-line. Solid bold
line is the position of the crest at the previous moment, t, and
the dashed bold line at the next moment, 
. The point C with
chosen coordinate s has shifted to C' with the velocity V normal to
the crest-line and G along the crest-line, and orientation of the crest-line at
that point has turned by the angle 
.
Then the required solution is
Now we transform (5) into the coordinate system
(11), and perform the substitution (12). Linear
approximation in 
yields
where the time-independent linear operator 
is
The translational symmetry of (5) means that has
two null-eigenfunctions
and far from the tip, the perturbed solution approaches the plane wave, so
In what follows, we shall assume that these limits are approached rapidly enough.
We introduce the following notations for local crest line-related
quantities (see also Fig. 1b): 
for unit tangent, 
for local
curvature, 
for normal velocity,
for tangent velocity and
for angular velocity.
It is easily seen that
We expect to find solutions depending on the small parameter 
not only through (12) but also via the shape of the crest line.
This dependence may be different in different
situations. To facilitate calculations, however, we stick to a certain
dependence, which will later prove to be a self-consistent assumption
in some cases, and still lead to correct consequences, if expressed in
original variables, in other cases (including the special case
corresponding to the `traditional' equations). Namely, we assume that
where the quantities with subscript 1 are supposed to remain finite
in the limit 
. A more generic and accurate
approach would consider each of these quantities as an independent
small parameter; however, this would only enlarge the formulae and yet
lead to the same results.
In a linear approximation in , the free term h in (13) is
Let us define the two-dimensional inner product,
Then the conditions of solvability of (13) with respect to 
are
where 
, 
are the null-eigenfunctions of the adjoint operator
,
We assume without proof, that asymptotic behaviour of 
at
large s is analogous to (17), i.e.
Now, we come to the key point in the derivation. Let us consider equation (22) for j=1:
It contains two singular integrals. Convergence of the first one is
provided by the decay of 
(17) and the boundedness
of other factors. On the contrary, convergence of the second one is not
guaranteed by any of the assumptions made so far. So, to satisfy
Eq. (25), we should first provide the convergence of this
integral, which requires that the integrand vanishes at large s. This
requirement leads immediately to the classical wave motion equation
(1), where
and the parentheses 
denote one-dimensional
inner products,
With (1), (26) satisfied, both integrals in (25) converge and we may further require that their sum vanishes. This leads to another equation, now for the tip:
where
Note, that we now have obtained two motion equations, one for the crest line (1) and one for the tip (28), out of single equation (25).
Equation (22) at j=2 also contains singular integrals, but their convergence is already guaranteed by (17) and (24). So, this equation leads to just one more condition,
where
Equations (28) and (32) give the required system of
equations at the wave tip and supplement the wave motion equation
(1). In this system, boundary conditions for K(s,t) and
equations of the tip motion are mixed together. With help of (18), it can be rewritten in an equivalent form
,
In original variables this is
where functions K, K', G and 
are assumed to have
arguments (0,t). Here the first equation is the boundary condition
for the evolution of K(s,t), and the two others determine the motion
of the tip given the evolution of K(s,t).
In these equations, we have retained terms of different asymptotical
orders in , to keep within the scope the traditional
equations (2), (3). Equation (2)
can be considered as a special case of (32) at 
.
Equation (28) is new, and is to replace the traditional
equation (3), which does not fit to the new system at all,
or requires too many assumptions to have sense. However, the stationary
versions of the motion equations are comparable, and will be compared
the next section and in Discussion.
