Voronin's Universality Theorem
This extraordinary 1975 result receives surprisingly little coverage (it was difficult to find a clear and accurate statement anywhere on the WWW in March 2004):
Let f(z) be any analytic function which is nonzero in the open disc |z| < r for some 0 < r < 1/4 and continuous up to the boundary of this disc. Then a disc of radius r centred on the line Re[s] = 3/4 can always be found in which the zeta function approximates the behaviour of f(z) in |z| < r, within any given accuracy.
In other words, given such an f(z), r and
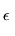 > 0, we can always find some real value t
such that
> 0, we can always find some real value t
such that
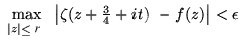
Note that through a simple translation and rescaling procedure, we can obtain as a corollary that the (nonzero) behaviour of any analytic function on any open disc in the complex plane can be reproduced with arbitrary accuracy by the zeta function acting on one of these discs of radius 1/4 in the right half of the critical strip.
This theorem first appeared here:
S.M. Voronin, "Theorem on the 'universality' of the Riemann zeta-function", Izv. Akad. Nauk SSSR, Ser. Matem. 39 (1975) (in Russian). English translation in: Math. USSR Izvestija 9 (1975) 443-453
This article of the same year appears to be related:
S.M. Voronin, "A theorem on the distribution of values of the Riemann zeta-function" (Russian), Dokl. Akad. Nauk SSSR 221 (1975) 771. English translation in Soviet Math. Dokl. 16 (1975) 410.
Universality is covered in this book:
A.A. Karatsuba and S.M. Voronin, The Riemann
Zeta-Function (de Gruyter, 1992)
On p. 377 of M.C. Gutzwiler's Chaos in Classical and Quantum Mechanics (Springer-Verlag, 1990), he writes:
"Although the Riemann zeta-function is an analytic function with [a] deceptively simple definition, it keeps bouncing around almost randomly without settling down to some regular asymptotic pattern. The Riemann zeta-function displays the essence of chaos in quantum mechanics, analytically smooth, and yet seemingly unpredictable.
This chaotic feature has been demonstrated more dramatically by Reich (1980) and Good (1981), in the form of the following amazing theorem:
Let D be a disk of radius r > 0 in the complex plane, centered on one of the points $\mu + im\nu$, where 1/2 < $\mu$ < 1 and $\nu$ > 0 are fixed, while the integers m > 0; the size r of these disks is limited by the condition that they have to be inside the strip 1/2 < z < 1; then choose an arbitrary non-vanishing, holomorphic function f(z), whose Taylor expansion around 0 converges inside a circle of radius r. Not consider the set M of integers m > 0, for which the difference $|f(z - \mu - im\nu) - \zeta(z)| < \epsilon$ in the whole disk around $\mu + im\nu$ for some fixed $\epsilon < 0$. This set is proved to have a non-vanishing density, i.e., the number of points in M below some large N > 0 is a non-vanishing fraction of N with a lower bound greater that 0; this fraction depends, of course, on the function f(z) and on $\epsilon$.In a more intuitive language, the Riemann zeta-function is capable of fitting any arbitrary smooth function over a finite disk with arbitary accuracy, and it does so with comparitive ease, since it repeats the performance like a good actor infinitely many times on a designated set of stages."
This is part of the book's section 19.9: "Chaos in Quantum-Mechanical Scattering" which relates to Selberg zeta functions a lot of the material in the scattering and number theory page.
This is from an article by Gutzwiller in Scientific American (January, 1992):
"The chaos of the Riemann zeta function is particularly apparent in
a theorem that has only recently been proved: the zeta function fits
locally any smooth function. The theorem suggests that the function
may describe all the chaotic behaviour a quantum system can exhibit."
A. Laurincikas, Limit Theorems for the Riemann Zeta-Function, (Kluwer, 1996)
[AMS review found here]
[review by M. Jutila:] "Several books on the Riemann zeta-function have appeared in recent years, but the present one seems to be the first devoted solely to its probabilistic aspects. Starting from the basis of standard university courses, this monograph provides an excellent introduction to topics like the value distribution of the zeta-function or its "universality" properties. To a considerable extent, the material covered represents the author's own research in probabilistic number theory. Illuminating additional information may be found in the notes after each chapter, and there is an extensive bibliography.
The necessary background from probability theory is given in Chapter 1.
Then the main objects of study, the Dirichlet series and polynomials,
are introduced in Chapter 2. Basic properties of Riemann's
zeta-function and Dirichlet's L-functions are surveyed; it may
be a bit misleading for a non-specialist that the zero-free region
for the zeta-function (in Theorem 8.6) is not given in the sharpest
known form. The actual topic of the book begins in Chapter 3 with
a discussion of limit theorems for the modulus of the zeta-function
in the half-plane Re[s] > 1/2 (in the first place near the
critical line). The theory of moments of the zeta-function (going back
to Ramachandra and Heath-Brown) plays an important role here. In the
next chapter, the value distribution of the zeta-function is studied
more generally. Chapter 5 deals with limit theorems of the
zeta-function in the space of analytic functions, as a preparation
for a proof of Voronin's universality theorem in Chapter 6. Then, in
Chapter 7, a limit theorem for the zeta-function in the space of
continuous functions is established under the assumption of the
Riemann hypothesis. In the last two chapters, preceding limit
theorems pertaining to the zeta-function are generalized to wider
classes of functions, first to Dirichlet L-functions, and finally
to Dirichlet series with multiplicative coefficients."
K. Bitar, "Path integrals and Voronin's theorem on the universality of the Riemann zeta function", Nucl. Phys. Proc. Suppl. 26 (1992) 656
[abstract:] "We explore a new approach to the path integral for a latticized quantum theory. This talk is based on work with N. Khuri and H. Ren."
The work in question is this:
K.M. Bitar, N.N. Khuri and H.C. Ren, "Path integrals and Voronin's theorem on the universality and the Riemann zeta function", Annals of Physics 67 (1991) 172-196
K. Bitar, N.N. Khuri and H.C. Ren, "Path integrals and discrete sums", Physical Review Letters 67 (1991) 781-784
K. Bitar, "A study of the Riemann zeta function" (online notes)
"The well known Riemann zeta function has many interesting properties and has proven to be useful in many applications in physics. In our attempt to use one such property, one described by Voronin's theorems, a new characteristic distribution was discovered numerically and then calculated analytically. This distribution allows the use of the Riemann zeta function as a generator of pseudo random numbers.
S.C. Woon, "Riemann zeta function is a fractal" (preprint 06/94)
"[We] infer three corollaries from Voronin's theorem [on the 'universality' of the Riemann zeta function]. The first is interesting, the second is a strange and amusing consequence, and the third is ludicrous and shocking (but a consequence nevertheless)."
"Corollary 1 ("interesting") Riemann zeta function is a fractal."
Woon's innovation here is to devise analytic function f based on the zeta function itself (involving translations and rescalings), in order to show that zeta replicates its own behaviour infinitely often at all scales.
"Since ao can be arbitrarily chosen, there are self-similarities at all scales. Therefore, Riemann zeta function is a fractal."
He goes on to show that you can choose f to be based on the zeta function not only via translation and dilation, but also invovling rotation and reflection. The result is that we have self-similarities between discs at different scales and orientations."
"Riemann zeta function is fractal in the sense that the Mandelbrot set is fractal (self-similarities between a region bounded by a closed loop C and other regions bounded by closed Cm' of the same shape at smaller scales and/or orientations). The fractal property of zeta is not "infinitely recursive" as in Koch snowflake. Such infinite recursions in a function will render the function non-differentiable, whereas zeta is infinitely differentiable. So, the manifold of zeta function is not of fractal dimension."
"All Dirichlet L-functions are also fractal. This follows from the remark following Voronin's theorem in Voronin's paper."
"Corollary 2 ("strange and amusing") Riemann zeta function is a 'library' of all possible smooth continuous line drawings in a plane."
Imagine all the ways an analytic function can map a line segment, say the vertical diameter of |z| < 1/4, into the complex plane. Woon points out that every imaginable kind of shape (an outline Mickey Mouse is used as an example) can be drawn in this way. It then follows from the Universality Theorem that the zeta function's behaviour on segments of Re[s] = 3/4 (or any other line between 1/2 and 1) can replicate any such shape.
"Corollary 3 ("ludicrous and shocking") Riemann zeta function is a concrete "representation" of the giant book of theorems referred to by Paul Halmos."
Woon explains that you can represent arbitrarily long Morse code messages as oscillating curves representing 'signals'. Every possible one of these messages is reproducible to within a workable accuracy by the zeta function. So the entire Encylopedia Britannica could be deduced as a Morse Code transmission encoded as a wave which was the image of a vertical segment of length 1/2 on Re[s] = 3/4 under the Riemann zeta function.
"So... the entire human knowledge are already encoded in zeta function."
"Hence, Riemann zeta function is probably one of the most remarkable functions because it is a concrete "representation" (in group theory sense) of "the God's giant book of theorems" that Paul Halmost spoke of - all possible theorems and texts are already encoded in some form in Riemann zeta function, and repeated infinitely many times. Although a white noise function and an infinite sequence of random digits are also concrete "representations", Riemann zeta function is not white noise or random but well-defined.
Alternatively, from the point of view of information theory, even though Riemann zeta function is well-defined, its mappings in the right half of the critical strip are random enough to encode arbitrary large amount of information - the "entropy" of its mapping is infinite.
Example This article is also encoded somewhere in Riemann zeta function as it is being written!"
S.C. Woon, "Fractals of the Julia and Mandelbrot sets of the Riemann zeta function" (preprint 12/98)
"Computations of the Julia and Mandelbrot sets of the Riemann zeta
function and observations of their properties are made. In the
appendix section, a corollary of Voronin's theorem is derived and a
scale-invariant equation for the bounds in Goldbach conjecture is
conjectured."
R. Garunkstis, "The effective universality theorem for the Riemann zeta-function" (preprint 02/03)
[abstract:] "It is known that Voronin's universality theorem for the Riemann zeta-function is ineffective. For some partial cases we obtain the effective version of this theorem."
Ineffective in this case means that upper bounds cannot be derived
for t as a function of 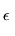 .
.
R. Garunkstis, "On the Voronin's universality theorem for the Riemann zeta-function"
[abstract:] "We present a slight modification of the Voronin's
proof for the universality of the Riemann zeta-function. The difference
(and simplification) is that we do not use the rearrangement of terms
in functional series."
[The following is based on AMS notes found here:]
Corresponding results for Dedekind zeta-functions, for all Dirichlet L-functions and other Dirichlet series, for Hurwitz and Lerch zeta-functions, for certain Euler products and other related functions were obtained by Voronin, Reich, Gonek, Laurincikas and co-workers and Bagchi.
Some functions were also found where the requirement that f be zero-free can be dropped; examples are the derivative of the Riemann zeta-function, log, Hurwitz and Lerch zeta-functions and others; see Gonek '79, Bagchi '81-'82, Gavrilov and Kanatnikov '82, Voronin '77, and Laurincikas and Garunkstis '97-'99. For treatments of these topics in textbooks refer to the 1992 and 1996 textbooks listed above.
A. Reich, "Universelle werteverteilung von Eulerprodukten", Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II (1977) 1-17
A. Reich, "Werteverteilung von zetafunktionen", Arch. Math. 34 (1980) 440-451
A. Reich, "Zur Universalität und Hypertranszendenz der Dedekindschen zetafunktion", Abh. Braunschweig. Wiss. Ges. 33 (1982) 197-203.
S.M. Gonek, "Analytic properties of zeta and L-functions", Thesis, Univ. of Michigan, Ann Arbor, 1979.
A. Laurincikas, "The universality theorem" (Russian), Litovsk. Mat. Sb. 23 no. 3 (1983) 53-62. English transl. in: Lithuanian Math. J. 23 (1983) 283-289
A. Laurincikas, "The universality theorem. II" (Russian), Litovsk. Mat. Sb. 24 no. 2 (1984) 113-121. English transl. in: Lithuanian Math. J. 24 (1984) 143-149
A. Laurincikas, "On the universality of the Riemann zeta-function" (Russian), Liet. Mat. Rink. 35 (1995) 502-507. English transl. in: Lithuanian Math. J. 35 (1995) 399-402
A. Laurincikas, "The universality of the Lerch zeta-function" (Russian), Liet. Mat. Rink. 37 (1997) 367-375. English transl. in: Lithuanian Math. J. 37 (1997), 275-280
A. Laurincikas, "On the Lerch zeta function with rational parameters" (Russian), Liet. Mat. Rink. 38 (1998), 113-124. English transl. in: Lithuanian Math. J. 38 (1998)
A. Laurincikas, "On the Matsumoto zeta-function", Acta Arith. 84 (1998) 1-16
A. Laurincikas and K. Matsumoto, "The universality of zeta-functions attached to certain cusp forms" (preprint)
A. Laurincikas, K. Matsumoto and J. Steuding, "The universality of L-functions associated with new forms", Izvestiya: Mathematics 67 no. 1 (2003) 77
B. Bagchi, "The statistical behaviour and universality properties of the Riemann zeta function and other allied Dirichlet series", Thesis, Indian Statistical Institute, Calcutta, 1981.
B. Bagchi, "A joint universality theorem for Dirichlet L-functions, Math. Z. 181 (1982), 319-334.
V.I. Gavrilov and A.N. Kanatnikov, "An example of a universal
holomorphic function" (Russian), Dokl. Akad. Nauk SSSR
65 (1982), 274-276. English transl. in: Soviet Math.
Dokl. 26 (1982), 52-54.
archive tutorial mystery new search home contact