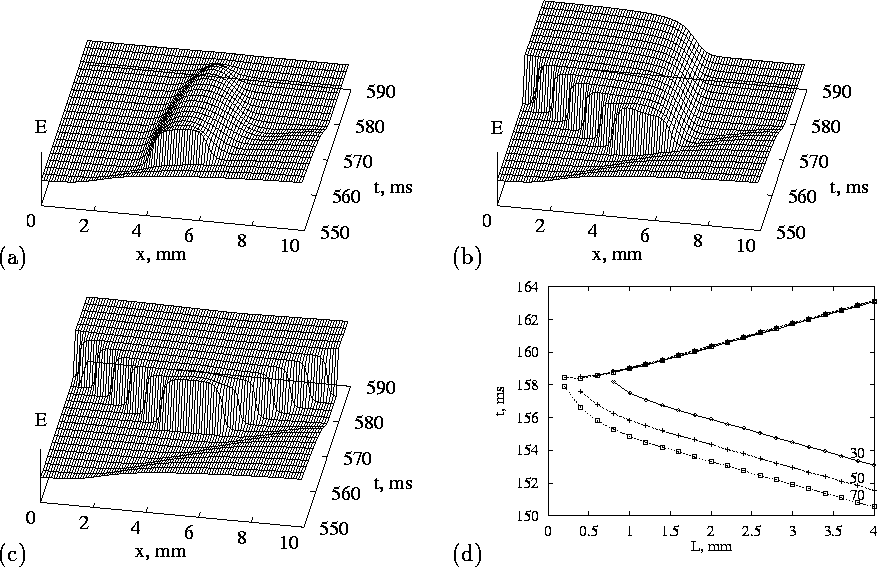
Figure 2: 1-D vulnerability in the OGPV model. Two conditioning pulses with the interval of
The reaction-diffusion equation (2) in one dimension has a spatially uniform solution, corresponding to resting tissue, and can support solitary wave and wave train solutions. The solitary travelling wave solution propagates at a velocity proportional to the square root of the diffusion coefficient, and so the diffusion coefficient can be chosen to give appropriate length and velocity scaling. Fig. 1(d) illustrates travelling wave train solutions; at the higher rate the action potential duration is shortened, and the action potential velocity is reduced, and the spatial extent (the ``wavelength'', say measured at 95% repolarisation) is shortened. Thus although there may not be enough room in the heart for more than one action potential at low rates, as rate is increased the shorter wavelength may allow more than one action potential.
Two travelling wave solutions meeting head on collide and annihilate each other; this destructive interference results from the refractory period of the travelling waves. Supra-threshold stimulation at a point in a uniformly resting one-dimensional model produces a pair of travelling wave solutions that propagate away from the initiation site. The initiation of a single solitary wave in a one-dimensional ring provides a computationally simple model for re-entry; such unidirectional propagation can only be produced in a homogeneous one-dimensional medium if the symmetry is broken, say by a preceding action potential. Fig. 2(a-c) illustrate the responses of a one dimensional ventricular tissue model to stimulation at different times in the wake of an action potential. The vulnerable window is the period after a preceding action potential during which a unidirectional wave in a one dimensional medium can be initiated; stimulation during the vulnerable period in the wake of a plane wave in a two-dimensional medium would initiate a pair of spiral waves. Thus the test pulse in Fig. 2(b) falls into the vulnerable window.

Figure 2:
1-D vulnerability in the OGPV model. Two conditioning pulses with the
interval of ![]() passed through the medium rightwards, then the test
pulse was delivered in the wake of the last conditioning wave.
(a)-(c) shows no, uni- and bi-directional responses to the test
stimuli of the same amplitude
passed through the medium rightwards, then the test
pulse was delivered in the wake of the last conditioning wave.
(a)-(c) shows no, uni- and bi-directional responses to the test
stimuli of the same amplitude ![]() of the
same
of the
same ![]() piece of the medium, but delivered at different time
moments. (d) shows vulnerable window (ordinate, earliest and latest
time delay after the start of the last conditioning wave) for
unidirectional response, as function of electrode size (abscissa) and
stimulus amplitude (shown as label on each line, mV/ms), with center of
the stimulated region fixed.
piece of the medium, but delivered at different time
moments. (d) shows vulnerable window (ordinate, earliest and latest
time delay after the start of the last conditioning wave) for
unidirectional response, as function of electrode size (abscissa) and
stimulus amplitude (shown as label on each line, mV/ms), with center of
the stimulated region fixed.
Starmer et al. [24] have characterised the vulnerable window for Beeler-Reuter and FitzHugh-Nagumo models. The numerical results of Fig. 2(d) show the expected increase in the vulnerable window with stimulus intensity and with the length of the stimulated tissue (the electrode size). If the effects of pharmacological agents or pathological processes (ischemia, acidosis) can be expressed as changes in the excitation system (1) then repeating the computations of Fig. 2 provides a means of quantifying the pro- or anti-arrhythmogenic effects of these changes.