Figure 3:
Snapshot of a spiral wave in the OGPV model. Gray-scale shading
codes the transmembrane voltage; white is activation and dark
is repolarisation.
Shown are two isolines, one of the voltage, 
(black
curve) and the the other of 
inactivation gate 
(white curve). Crossing of the two isolines is the instant position
of the spiral tip (big black circle). The flower-like line made of small
white circles is the trajectory of the tip in the last few
rotations.
Figure 3 illustrates a spiral wave solution of the model, as
the spatial distribution of the membrane potential V, at an instant
after the spiral wave was initiated by cutting a broken plane
wave half way up the medium. The wavefront of the action potential is
the sharp transition between light and dark shade, and far from the tip
of the spiral the wavelength of the spiral (the distance between
successive wavefronts) is about 
. The spiral rotated with an
initial period of approximately 
, and over the first 
the
period decreased to 
. The tip of the spiral may be defined
by the intersection of two isolines; we define the tip by the
intersection of the and the f=0.5 isolines, where
f is the 
(slow inward) current inactivation gating variable. The
trajectory of the tip of the spiral is not stationary, but meanders,
and its motion is nonuniform, moving by a jump-like alternation between
fast and very slow phases, with about 5 jumps per full rotation. This
motion resembles an irregular, nearly biperiodic process, with the
ratio of the two periods close to 1:5.
The rotation of the spiral wave can be monitored by following an isoline on the wavefront, and the trajectory of the tip of the spiral, as illustrated in Fig. 3. The area enclosed by the tip trajectory is analogous to the core of a rigidly rotating spiral, and is not invaded by the action potential. Characteristics of the V(t) observed at different sites in the medium during the evolution of a rotating spiral wave are (see Fig. 4 or [19] for more detail):
, but
appears more as complicated oscillations than action potentials.
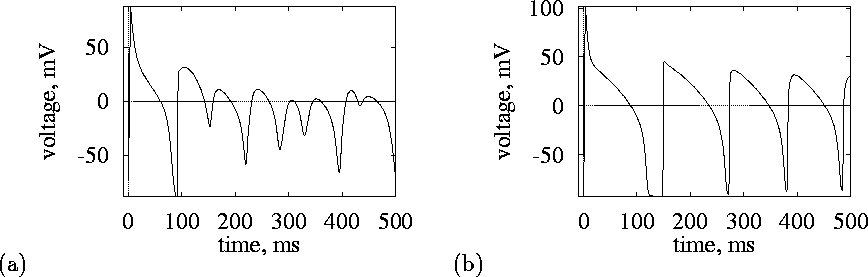
Figure 4:
Transmembrane voltage recorded inside (a) and outside (b)
the core.
These different behaviours occur in an initially homogeneous medium, in which re-entry has established a functional inhomogeneity, and are similar to the behaviours of all functional re-entry waves in excitable medium, and to waves in excitable media rotating around a small obstacle.
Within the functional block or core the membrane potential remains
between -45 and 
; this persistent depolarisation means the inward
is inactivated, blocking propagation into the core. The
principal currents 
far from, and within
the core are examined in [19].
After an initial transient, the spiral is rotating around a compact core contained within a few mm square. The multi-lobed pattern of the trajectory of the tip illustrated in Fig. 3 takes time to develop, and itself continues to develop with time. This time evolution, or ``aging'' is described in [19] and has been ascribed to the slow changes in intracellular concentrations that occur in the Oxsoft models.
Figure 5:
Development and aging of a spiral wave after initiation by phase
distribution initial conditions. Two left columns show successive 1- 
\
isochronal maps; the right columns shows corresponding pieces of tip
trajectory. Square size 
.
A different approach to examining this aging appears by plotting the voltage isochrones every ms, as in Fig. 5. Here the spiral was initiated from initial conditions specified by the phase distribution method, to prevent any extended structures being produced by the method of initiation of the spiral. Close to the tip of the spiral the distance between the isochrones changes, and so the local wavefront velocity is changing, with slow velocities occurring at the sharp turns of the tip. Bunching of isochronal lines is interpreted as an arc of conduction block in clinical cardiac mapping studies. The spirals initiated from a broken wave and by the cross field technique have more pronounced transients, and their tip evolution is described in [19]. The pattern of the tip motion and the associated velocity of the wavefront near the tip is continually changing, and the early tip trajectory resembles the linear extended tip trajectories seen in the Beeler-Reuter model [25]. However, the slowing down occurs along the linear segments of the trajectory, as well as at the sharp corners.
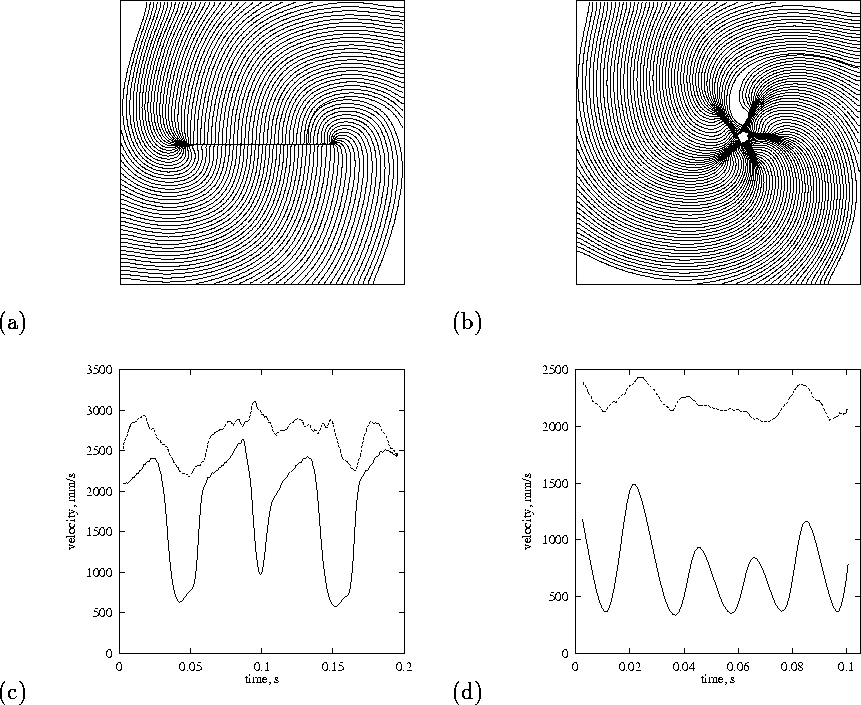
Figure 6:
Nonuniformity of propagation velocity around a hole (left column) and
in a spiral wave (right column). Top: isochronal map of one rotation
with 
step between isochrones. Bottom: variation of propagation
velocity with time during the rotation; solid line at the distance
and the dashed line at 
from the tip along the
isochrones. Square size .
Girouard et al. [7] have studied propagation of re-entrant waves around a laser induced linear obstacle in the guinea-pig heart. Fig. 6 compares propagation around a thin linear obstacle, with propagation around a functional block. The isochronal maps show the slowed propagation associated with the sharp turns, and the local normal wavefront propagation velocity. For the obstacle, the slowing down is confined to the ends of the obstacle, where the curvature is large, and is consistent with the observations of Girouard et al. [7]. For the functional block there is not a clear connection between the curvature and the velocity.
We believe that around the obstacle, the slowing down is predominantly
due to curvature effects, while for the functional block the dominant
effect is the propagation of the wavefront into a region of refractory
tissue. Although the wavefront, driven only by { 
current, cannot
propagate deep into a region where this current is inactivated,
current can carry the wavefront into refractory region. This is
analogous to the interpretation of the onset of irregularity in
re-entry in the Beeler-Reuter model as due to interactions between {
and activation fronts [26]. Explicit
initiation of { and propagation fronts in Beeler-Reuter model has
been done by Romashko and Starmer [27];
however, direct observation of fronts in electrophysiological
experiments is difficult as normally both { and currents are
essential for propagation and pure fronts occur only in special
circumstances and are characterised by lower gradients and propagation
speed [28].
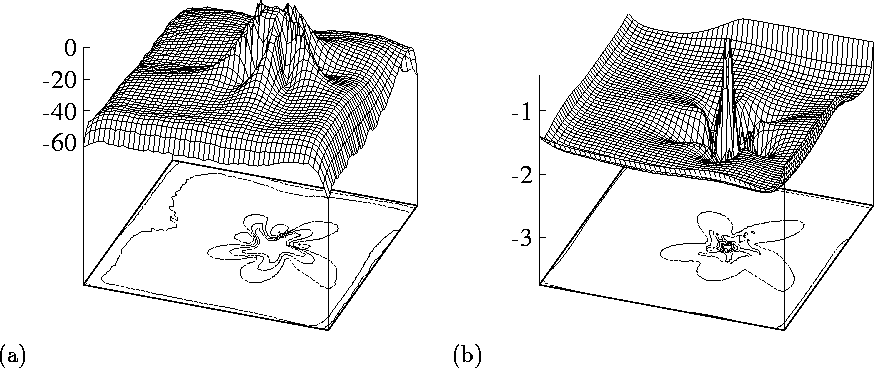
Figure 7:
The role of the two major excitatory currents, 
(left) and
(right), in forming the shape of the core. Shown are the
distribution of the minimal (i.e. maximal in the absolute value)
currents throughout the preparation during 
, i.e. slightly
longer that one rotation of the spiral wave, same as shown in
Fig. 6(b). Vertical axes show values of the
currents in nA per cell. Square size .
This interpretation can be illustrated by blocking
-conductance, which removes the extended conduction
blocks[26], or by visualising the maximum currents
during one rotation. Fig. 7 shows the maximal magnitude
of the principal depolarising currents, and during
just over one rotation, the same computation as in
Fig. 6(b).
While sodium current shows the five-petal star shape of the block (the
region where it was nearly zero throughout the rotation), the calcium
current has small circular block and only a slight surrounding modulation.
Thus, the meandering petals can be interpreted as loci where fast
sodium waves died out and propagation was supported by slow calcium
waves. The five-lobed pattern is not an attractor, as its shape is
continually and slowly changing. However it is persistent for long
enough to be considered the state of the spiral wave we would seek to
eliminate in section 5; it is important to note that its behaviour and
evolution can be understood in terms of the dynamic balancing between
the fast and slow depolarising currents, rather than simple curvature
and electrotonic loading effects.