First we verify the quasi-stationary exclusion of the small parameter
in transforming from (15) to (19) by studying
the excitation processes in these two systems, and accuracy of the
two-point approximation in (21) by comparision
with the results of the five-compartment model (22). The
kinetics f(), g() and h() were described by guinea pig ventricle
myocyte model of Noble et al. [1990], that has 17 kinetic variables.
was 10 
S, which is consistent with data of Plonsey &
and Barr [1986]. In the vector v we included the three fastest gating
variables `h', `d' and `f'; gate `m' was not a dynamic variable but a
fixed function of u. Thus, model (19) contained 20 ODEs, as
opposed to 34 ODEs and large values of the parameters and
in (15), and 29 ODEs in the five-compartment
version (22).
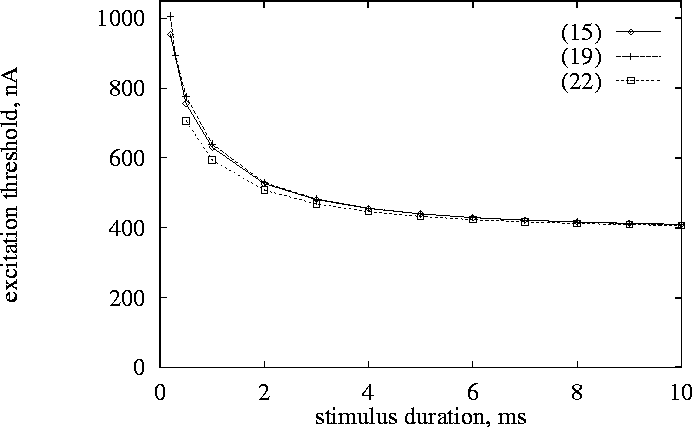
Figure 1:
Strength-duration curve for a single isolated cell excited by an
extracellular current pulse. 
: computed
with two-point evaluation of integral, model (15). + : quasi-stationary
model (19), 
: computed with five-point evaluation of integral, model (22).
We obtained the strength-duration curve -- the threshold external
current as a function of
stimulus duration (Fig. 1).
The results obtained for the three models (15),
(19) and (22) coincide with a good precision. Thus
is large enough for the quasi-stationary approximation to be
valid, and two-point evaluation of the surface integral gives
reasonable accuracy, and in all other numerical experiments we used
only model (19).
Figure 2:
Excitation threshold of a single cell excited by an extracellular
current pulse of 2 ms duration computed using model (19), as a function of time since the
beginning of the last conditioning action potential, in model (19). To ensure that the state variables
were close to those found during re-entry, the cell was conditioned by
a train of action potentials obtained from a re-entrant spiral
solution; the inter-wave interval is the interval between the minimum
of u of the previous excitable gap, to the start of the current
pulse.
The threshold current was also determined at a stimulus duration of 2 ms and different intervals after a preceding action potential. The excitability of the biophysical excitation equations for cardiac tissue is highly dependent on the history of the cell activity. Intervals between action potentials as short as those in Fig. 2 cannot be achieved by a pair of stimuli applied to a resting cell, as they are less than the standard (from rest) action potential duration. Since we are specially interested in the defibrillation threshold, the cell has been preconditioned by an excitation sequence identical to that of a point in a developing spiral wave during first 14 rotations; in this model, the average period of the spiral wave is around 102 ms.