One of necessary conditions for the results of previous subsection is
that parameter 
is nonzero -- and, moreover, is negative. Let us
consider the special case
Now we look for solutions to the finite problem (47) in the form
at the J-branch, where 
is the least positive root
of equation
Then 
and hence
boundary conditions (47) become
where 
. This gives
and the dimensional parameters of the spiral wave solution are
This solution formally coincides, in the main orders, with that presented in [10, 11]:
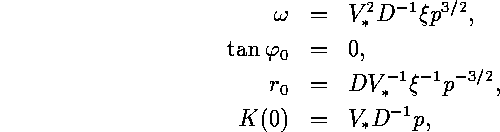
where p is a small parameter and 
was found by
numerical integration of equation (38). This coincidence is
achieved by identifying p with 
and
with 
. In this `weak' sense we
can say that the `traditional' case is of codimension 1 relative to the
generic case, as the `traditional' spiral wave solution can be achieved
if one additional conditions (61) is fulfilled. Note, however,
that this is only a formal correspondence, as the small parameter
p of [10, 11] has different physical sense from
: while shows the instantaneous turning rate of a tip of
an uncurved half-wave, with its growth rate being zero in this case, p is
proportional to the growth rate while the turning rate is assumed
identically zero. This is because coincidence of the solutions
was achived not by coincidence of equations.
