Problem formulation and general solution.

A stationary spiral wave rotates rigidly around a fixed point, and its tip describes a circle, called the core of the spiral, centered at that point. The rigid rotation means that the shape of the wave remains constant and only its position on the plane changes, so K and G do not depend on t. In this case, the wave evolution equation (1) can be transformed to an integro-differential one [10, 11],

 

where is now the constant angular velocity of the whole spiral; for definiteness we consider only spirals rotating counter-clockwise, so that increasing s means moving from left to right with respect to propagation direction, and .

The boundary conditions of (38) at s=0 are (37), and at infinity

 

Make a change of variables,

 

We are interested in solutions with K, and hence y, small. Transformation of equation (38) to an ODE and substitution (40) lead to the following equation:

 

where prime ' denotes differentiation by the new independent variable , with boundary conditions

  

This poses a nonlinear eigenvalue problem for eigenvalue and function . Here the dimensionless medium parameters are defined as

 

  
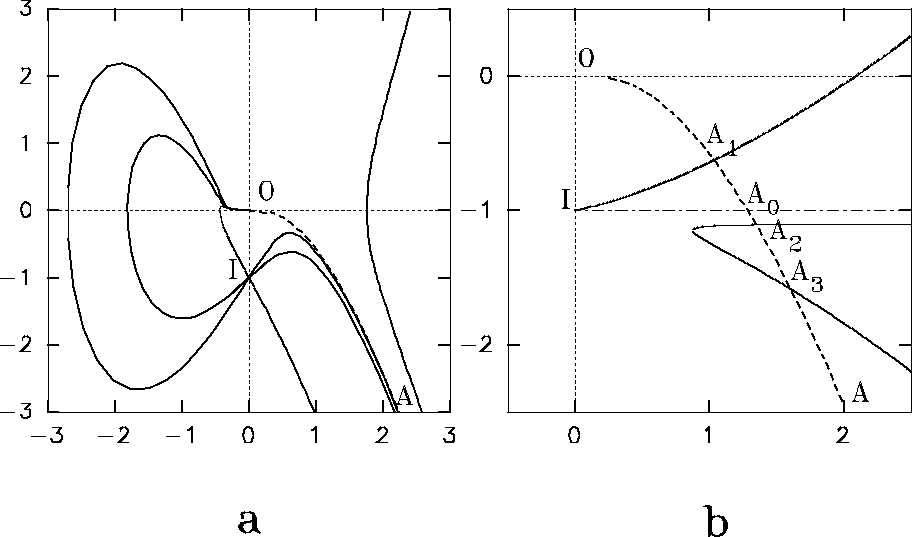
Figure 2: a Phase portrait of equation (41) in coordinates . O is a complex equilibrium, I is a non-equilibrium singular point. Dashed line OA is the separatrix of the origin. b The boundary-value problem in the same coordinates. The separatrix OA (dashed) is the only integral curve, obeying (43); conditions (42) select points on it, corresponding to the tip. Dash-dotted line IA corresponds to (2,3) and gives the only intersection point A . Solid lines correspond to , , , , , . In this case, there are three intersections, A, and thus three solutions, , -0.64050, -0.49185, and , 2.2233, 0.12060.

A phase portrait of the differential equation (41) without the term is shown on Fig. 2a. The only integral curve obeying the condition at infinity (43) is the separatrix OA. This curve can be described analytically; it is convenient to do that in a piecewise manner,

 

for , and

 

for , where is an integration constant related to the position of the tip point on the separatrix OA. We will call these pieces the J-branch and the I-branch respectively (it is easy to see that one is the analytical continuation of the other).

The tip point ( ) may be at the J-branch if or at the I-branch if , in the latter case only the I-branch plays a rôle. Boundary conditions at the tip from (42) in these two cases are

 

where the upper sign is for J-branch and lower sign is for I-branch,

 

and is the corresponding function from (45) or from (46).

So (47) is a system of finite (non-differential) equations for unknown variables and , which, in principle, solves the problem. All kinematical parameters of the spiral wave are expressed via and :

 

Here is the core radius and is the orientation angle of the tip with respect to its radius-vector.

System (47) in its general form is, however, rather complicated:

• The first of these equations is a cubic equation with respect to , and there may be up to three different spiral wave solutions in the same medium.
• Functions are transcendental, and explicit expression for cannot be written for the general case.
• It depends on small parameter and should have solution with uniformly small , and the problem is still more complicated if there are small parameters besides .

Fig. 2b illustrates these difficulties: it shows an example with three solutions, while two of them have y(0) small.

In following subsections, we consider two most important special cases, where explicit results can be obtained.