random matrices and the Riemann zeta function
There exist important conjectures which relate the statistical behaviour of the nontrivial zeros of the Riemann zeta function to the statistical behaviour of the eigenvalues of large random matrices.
Although an individual matrix with fixed entries cannot meaningfully be said to be 'random', it is possible to precisely define 'random matrix ensembles' in terms of probability distributions.
Most relevant here is the Gaussian unitary ensemble, or GUE. Two equivalent ways of defining this for a given matrix dimension N are given here:
(1) M.L. Mehta (in his seminal book Random Matrices) starts with the space of all N x N Hermitian matrices, and introduces a probability density P on the space. Two conditions are given which P must satisfy, including invariance under unitary conjugation transformations H -> U-1HU on the space (here U is a fixed N x N unitary matrix).
It turns out that the conditions given force P(H) to take the form

Note the 'Gaussian' character of this distribution.
Accepting this definition, we see that there really is no such condition as being 'a GUE matrix'. The GUE consists of all Hermitian N x N matrices, but they are 'weighted' according to the probability density P.
I sometimes find it helpful to think of the GUE as 'a random matrix generator' which produces N x N Hermitian matrices with a probabilistic bias based on the function P. Any Hermitian matrix of dimension N can be produced, but some will occur more frequently than others. We are going to be looking at statistical tendencies in the behaviour of the eigenvalues of the 'output' of the generator. We will be particularly interested in what happens to these tendencies when we let N tend to infinity.
(2) An equivalent definition is provided by Andrew Odlyzko in his unpublished 1992 paper "The 1020-th zero of the Riemann zeta function and 175 million of its neighbors":
Despite the comments above, the idea is to construct a sort of 'archetypal GUE matrix' built from matrix entries involving Gaussian random variables:
We note that the diagonal elements of a Hermitian matrix must be real, and that the (complex) above-diagonal elements determine the (complex) below-diagonal elements via complex conjugation. Hence we can parametrise our N x N Hermitian matrix in terms of a fixed number of real variables (one for each diagonal element, and two for each above-diagonal element - a total of N2 parameters).
Having introduced a 21/2 scaling factor into the real variables representing diagonal elements (for technical reasons), all of the real parameters are assumed to be independent standard normal variables. Recall that this means they distribute according to the Gaussian distribution with zero mean and variance 1.
Again, it's important to stress the fact that any Hermitian
N x N matrix could be said to 'belong' to the GUE according to this
(equivalent) definition, but the involvement
of probability distributions guarantees that some are 'more likely
to show up' than others, according to a very particular law of
distribution.
A couple of excellently composed and well-referenced introductions to the relationship between the GUE and the Riemann zeta function:
Steven Finch's notes "GUE hypothesis regarding zeta function spacings"
D. Rockmore and D.L. Snell, "Chance in the Primes, Part III", Chance News
These are complemented by Dan Bump's commentary on the Gaussian Unitary Ensemble Hypothesis, which is a more casual, less technical affair explaining the connections with physics and the Riemann Hypothesis.
I would recommend these three sources (and Mehta's book) for a thorough
account of these matters. The commentary immediately below stresses a few points
which may help to assist in understanding the main ideas.
Asymptotically, the locations of the nontrivial zeros of the Riemann zeta function distribute in the critical strip according to a fairly simple logarithmic law, much like the primes do along the real line. Whereas the primes tend to become increasingly spaced out at a logarithmic rate, the zeta zeros tend to become more dense.
In order to undertake the most useful statistical analysis of the zeta zeros, it is necessary to 'normalise' them, by applying an appropriate rescaling. The idea is to cause the average spacing between consecutive normalised zeros to equal 1. We can then consider the distribution of these normalised spacings (a countably infinite set of positive values which tend to cluster around the value 1).
Similarly, given a Hermitian matrix of (large) dimension N, as we ascend the spectrum of eigenvalues we find an tendency towards increasing density between larger eigenvalues. This effect can be cancelled by rescaling to produce 'normalised eigenvalues' whose 'average consecutive spacing' is equal to 1. In this way, we can compute the distribution of spacings between consecutive normalised eigenvalues over the entire GUE of N x N Hermitian matrices. Remember that although this computation will involve all N x N Hermitian matrices, there is a 'weighting' so some will have a more significant effect than others.
In his aforementioned paper, Odlyzko sums up the situation:
"The basic results about distribution of GUE eigenvalues are completely rigorous. However, they do have many gaps. One of them is that the results are obtained by averaging over the full ensemble of GUE matrices. It is conjectured that if one considers a large random GUE matrix, the distribution of its eigenvalues will be close to that of the entire ensemble with high probability. Although numerical calculations confirm this conjecture, there is no proof of it."
The GUE Hypothesis, also known as the Odlyzko-Montgomery Law, states that these two 'consecutive normalised spacing' distributions (zeta zeros and GUE eigenvalues) are identical. In other words, the nontrivial zeros of the Riemann zeta function and the eigenvalues of GUE matrices share a particular 'statistical fingerprint'. This hypothesis was inspired by some theoretical work of Montgomery, and backed up by a huge body of experimental evidence provided by Odlyzko.
[Note: In Steve Finch's notes it is pointed out that there is a slight technicality involving the use of only the eigenvalues in the central part or "bulk" of GUE spectra.]
Previous evidence of the nontrivial zeros of the Riemann zeta function
behaving like eigenvalues appeared in
the early 1950's when Selberg produced his trace formula.
This possiblity, that the zeta zeros are 'spectral in nature',
is particularly attractive to those trying to prove
the Riemann Hypothesis via the suggestion of Hilbert and Pólya.
It is possible to give an explicit expression for this probability distribution which both GUE eigenvalue spacings and zeta zero spacings are conjectured to follow:
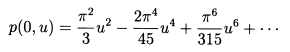
There is a sequence of distributions {p(k,u)} of which this is the first. These can all be expressed as power series, and are such that
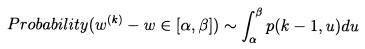
Here w(k) denotes the kth normalised eigenvalue (or zeta zero) to be greater than a given normalised eigenvalue (or zeta zero) w. The probability that w(k) lies at a distance beyond w between a given pair of limits is equal to the area under the graph of p(k-1,u) between the same limits.
Note that w(1) is the first normalised eigenvalue (or zeta zero) to be greater than w, hence w(1) - w is the distance between consecutive normalised eigenvalues (or zeta zeros) which is what we have been discussing above. It therefore makes sense that

A further prediction, which Odlyzko refers to as the Montgomery pair correlation conjecture, deals with another statistical similarity seemingly shared by the zeta zeros and the GUE eigenvalues.

Here we see a graph of the function
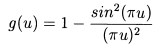
The idea, essentially, is this. Given a normalised zeta zero, and a pair of positive values a, b with a < b, we can consider the number of zeta zeros whose 'heights' above the given zero are between a and b. Montgomery has conjectured that the mean value of such quantity (taken over the whole set of nontrivial zeta zeros) will equal the area under the graph of g(r) between limits a and b (i.e. the integral of g between these limits).
Exactly analogous behaviour had been discovered in the context of random matrix theory by Freeman Dyson, who had been investigating the possibility of using random matrices to model the behaviour of heavy nuclei. Montgomery and Dyson coincidentally became aware of the similarity in each others' work in 1972 while talking informally over tea at Princeton where Montgomery was a visitor.
[excerpt from K. Sabbagh's Dr. Riemann's Zeros (Atlantic, 2002), on this incident]
The fact that the graph of g descends rapidly as we approach zero means that the expection values for the numbers of zeta zeros in regions close to a given zero will rapidly dwindle as we approach zero. It is often said that this suggests a 'repulsion' between zeros, unlike Poisson (purely random) spacing statistics.
Note that we can relate the Montgomery pairwise correlation conjecture to the Montgomery-Odlyzko Law discussed above. We see that

since the expectation value of the number of eigenvalues (or zeta zeros) in a
particular interval 'above' a given eigenvalue (or zeta zero) will equal
the sum of probabilities of finding the first, second, third,... eigenvalue
(or zeta zero) in this interval.
F.W.K. Firk and S.J. Miller, "Nuclei, primes and the random matrix connection" (preprint 09/2009)
[abstract:] "In this article, we discuss the remarkable connection between two very different fields, number theory and nuclear physics. We describe the essential aspects of these fields, the quantities studied, and how insights in one have been fruitfully applied in the other. The exciting branch of modern mathematics, random matrix theory, provides the connection between the two fields. We assume no detailed knowledge of number theory, nuclear physics, or random matrix theory; all that is required is some familiarity with linear algebra and probability theory, as well as some results from complex analysis. Our goal is to provide the inquisitive reader with a sound overview of the subjects, placing them in their historical context in a way that is not traditionally given in the popular and technical surveys."
O. Barrett, P. Burkhardt, J. DeWitt, R. Dorward and S.J. Miller, "One-Level density for holomorphic cusp forms of arbitrary level" (preprint 04/2016)
"In 2000 Iwaniec, Luo, and Sarnak proved for certain families of $L$-functions associated to holomorphic newforms of square-free level that, under the Generalized Riemann Hypothesis, as the conductors tend to infinity the one-level density of their zeros matches the one-level density of eigenvalues of large random matrices from certain classical compact groups in the appropriate scaling limit. We remove the square-free restriction by obtaining a trace formula for arbitrary level by using a basis developed by Blomer and Milicevic, which is of use for other problems as well."
Note: a possible connection between g(r)
and Fibonacci numbers?
[more references can be found in Finch's notes]
H. Montgomery, "The pair correlation of zeros of the zeta function",
Analytic Number Theory (Proceedings of Symposia in Pure Mathematics
24) (1973) 181-193.
J.P. Keating and N.C. Snaith, "Random matrix theory and zeta(1/2 + it)", Communications in Mathematical Physics 214 (2000) 57-89.
This paper is based on part of Nina Snaith's doctoral research. Her Ph.D. thesis is available here in PostScript format - the initial chapters serve as an excellent introduction to this whole area of study.
J.P. Keating and N.C. Snaith,
"Random matrix theory and L-functions at
s = 1/2", Communications in Mathematical Physics 214
(2000) 91-110.
E. Strahov, "Moments of characteristic polynomials enumerate two-rowed lexicographic arrays"
[Abstract] "A combinatorial interpretation is provided for the moments of
characteristic polynomials of random unitary matrices. This leads to a rather unexpected
consequence of the Keating and Snaith conjecture: the moments of
$|\zeta(1/2+it)|$ turn out to be connected with some increasing subsequences
problems (such as the last passage percolation problem).
E. Bogomolny and J.P. Keating, "Random matrix theory and the Riemann zeros I: three- and four-point correlations", Nonlinearity, 8 (1995) 1115–1131.
E. Bogomolny and J.P. Keating, "A method for calculating spectral statistics based on random-matrix universality with an application to the three-point correlations of the Riemann zeros", Journal of Physics A 46 (2013) 305203
[abstract:] "We illustrate a general method for calculating spectral statistics that combines the universal (random matrix theory limit) and the non-universal (trace-formula-related) contributions by giving a heuristic derivation of the three-point correlation function for the zeros of the Riemann zeta function. The main idea is to construct a generalized Hermitian random matrix ensemble whose mean eigenvalue density coincides with a large but finite portion of the actual density of the spectrum or the Riemann zeros. Averaging the random matrix result over remaining oscillatory terms related, in the case of the zeta function, to small primes leads to a formula for the three-point correlation function that is in agreement with results from other heuristic methods. This provides support for these different methods. The advantage of the approach we set out here is that it incorporates the determinental structure of the random matrix limit."
E. Bogomolny and J.P. Keating, "Two-point correlation function for Dirichlet $L$- functions", Journal of Physics A 46 (2013) 095202
[abstract:] "The two-point correlation function for the zeros of Dirichlet $L$-functions at a height $E$ on the critical line is calculated heuristically using a generalization of the Hardy–Littlewood conjecture for pairs of primes in arithmetic progression. The result matches the conjectured random-matrix form in the limit as $E\rightarrow\infty$ and, importantly, includes finite-$E$ corrections. These finite-$E$ corrections differ from those in the case of the Riemann zeta-function, obtained in (1996 Phys. Rev. Lett. 77 1472), by certain finite products of primes which divide the modulus of the primitive character used to construct the $L$-function in question."
Y.Y. Atas, E. Bogomolny, O. Giraud, P. Vivo and E. Vivo, "Joint probability densities of level spacing ratios in random matrices" (preprint 05/2013)
[abstract:] "We calculate analytically, for finite-size matrices, joint probability densities of ratios of level spacings in ensembles of random matrices characterized by their associated confining potential. We focus on the ratios of two spacings between three consecutive real eigenvalues, as well as certain generalizations such as the overlapping ratios. The resulting formulas are further analyzed in detail in two specific cases: the beta-Hermite and the beta-Laguerre cases, for which we offer explicit calculations for small $N$. The analytical results are in excellent agreement with numerical simulations of usual random matrix ensembles, and with the level statistics of a quantum many-body lattice model and zeros of the Riemann zeta function."
O. Bohigas, P. Leboeuf, M. Sanchez, "On the distribution of the total energy of a system on non-interacting fermions: random matrix and semiclassical estimates"
"A semiclassical formula describing, as a function of n, a non-universal behavior of the variance of the total energy starting at a critical number of particles is...obtained. It is illustrated with the particular case of single particle energies given by the imaginary part of the zeros of the Riemann zeta function on the critical line."
O. Bohigas, P. Leboeuf, and M.-J. Sanchez, "Spectral spacing correlations for chaotic and disordered systems"
"New aspects of spectral fluctuations of (quantum) chaotic and diffusive systems are considered, namely autocorrelations of the spacing between consecutive levels or spacing autocovariances. They can be viewed as a discretized two point correlation function. Their behavior results from two different contributions. One corresponds to (universal) random matrix eigenvalue fluctuations, the other to diffusive or chaotic characteristics of the corresponding classical motion. A closed formula expressing spacing autocovariances in terms of classical dynamical zeta functions, including the Perron-Frobenius operator, is derived. It leads to a simple interpretation in terms of classical resonances. The theory is applied to zeros of the Riemann zeta function. A striking correspondence between the associated classical dynamical zeta functions and the Riemann zeta itself is found. This induces a resurgence phenomenon where the lowest Riemann zeros appear replicated an infinite number of times as resonances and sub-resonances in the spacing autocovariances. The theoretical results are confirmed by existing "data". The present work further extends the already well known semiclassical interpretation of properties of Riemann zeros."
P. Leboeuf, A. G. Monastra and O. Bohigas, "The Riemannium", Regular and Chaotic Dynamics 6 (2001) 205-210.
[abstract:] "The properties of a fictitious, fermionic, many-body system based on the complex zeros of the Riemann zeta function are studied. The imaginary part of the zeros are interpreted as mean-field single-particle energies, and one fills them up to a Fermi energy EF. The distribution of the total energy is shown to be non-Gaussian, asymmetric, and independent of EF in the limit EF -> infinity. The moments of the limit distribution are computed analytically. The autocorrelation function, the finite energy corrections, and a comparison with random matrix theory are also discussed."
P. Leboeuf and A.G. Monastra, "Quantum thermodynamic fluctuations of a chaotic Fermi-gas model"
[abstract:] "We investigate the thermodynamics of a Fermi gas whose single-particle energy levels are given by the complex zeros of the Riemann zeta function. This is a model for a gas, and in particular for an atomic nucleus, with an underlying fully chaotic classical dynamics. The probability distributions of the quantum fluctuations of the grand potential and entropy of the gas are computed as a function of temperature and compared, with good agreement, with general predictions obtained from random matrix theory and periodic orbit theory (based on prime numbers). In each case the universal and non-universal regimes are identified."
O. Bohigas and M.-J. Giannoni, "Chaotic Motions and Random Matrix Theories", Lecture Notes in Physics 209 (Springer-Verlag, 1984) 1-99.
E. Bogomolny, O. Bohigas, P. Leboeuf, A. G. Monastra, "On the spacing distribution of the Riemann zeros: corrections to the asymptotic result" (preprint 02/2006)
[abstract:] "It has been conjectured that the statistical properties of zeros of the Riemann zeta
function near $z = 1/2 + \ui E$ tend, as $E \to \infty$, to the distribution of eigenvalues of large
random matrices from the Unitary Ensemble. At finite $E$ numerical results show that the nearest-neighbour
spacing distribution presents deviations with respect to the conjectured asymptotic form. We give here
arguments indicating that to leading order these deviations are the same as those of unitary random matrices
of finite dimension $N_{\rm eff}=\log(E/2\pi)/\sqrt{12 \Lambda}$, where $\Lambda=1.57314 ...$ is a well
defined constant."
P. Forrester and A. Odlyzko, "A nonlinear equation and its application to nearest neighbor spacings for zeros of the zeta function and eigenvalues of random matrices"
[abstract:] "A nonlinear equation generalizing the $\omega$ form of the Painleve V equation is used to compute the probability density function for the distance from an eigenvalue of a matrix from the GUE ensemble to the eigenvalue nearest to it. (The classical results concern distribution of the distances between consecutive eigenvalues.) Comparisons are made with the corresponding distribution for zeros of the Riemann zeta function, which are conjectured to behave like eigenvalues of large random GUE matrices."
P.J. Forrester, "Diffusion processes and the asymptotic bulk gap probability for the real Ginibre ensemble" (preprint 06/2013)
[abstract:] "It is known that the bulk scaling limit of the real eigenvalues for the real Ginibre ensemble is equal in distribution to the rescaled $t \to \infty$ limit of the annihilation process $A + A \to \emptyset$. Furthermore, deleting each particle at random in the rescaled $t \to \infty$ limit of the coalescence process $A + A \to A$, a process equal in distribution to the annihilation process results. We use these inter-relationships to deduce from the existing literature the asymptotic small and large distance form of the gap probability for the real Ginibre ensemble. In particular, the leading form of the latter is shown to be equal to $\exp(-(\zeta(3/2)/(2 \sqrt{2 \pi}))s)$, where $s$ denotes the gap size and $\zeta(z)$ denotes the Riemann zeta function. A determinant formula is derived for the gap probability in the finite $N$ case, and this is used to illustrate the asymptotic formulas against numerical computations."
P.J. Forrester and A. Mays, "Finite size corrections in random matrix theory and Odlyzko's data set for the Riemann zeros" (preprint 07/2015)
[abstract:] "Odlyzko has computed a data set listing more than 109 successive Riemann zeros, starting at a zero number beyond 1023. The data set relates to random matrix theory since, according to the Montgomery—Odlyzko law, the statistical properties of the large Riemann zeros agree with the statistical properties of the eigenvalues of large random Hermitian matrices. Moreover, Keating and Snaith, and then Bogomolny and collaborators, have used $N\times N$ random unitary matrices to analyse deviations from this law. We contribute to this line of study in two ways. First, we point out that a natural process to apply to the data set is to thin it by deleting each member independently with some specified probability, and we proceed to compute empirical two-point correlation functions and nearest neighbour spacings in this setting. Second, we show how to characterise the order $1/N^2$ correction term to the spacing distribution for random unitary matrices in terms of a second order differential equation with coefficients that are Painlevé transcendents, and where the thinning parameter appears only in the boundary condition. This equation can be solved numerically using a power series method. Comparison with the Riemann zero data shows accurate agreement."
F. Bornemann, P.J. Forrester and A. Mays, "Finite size effects for spacing distributions in random matrix theory: Circular ensembles and Riemann zeros" (preprint 08/2016)
[abstract:] "According to Dyson's three fold way, from the viewpoint of global time reversal symmetry there are three circular ensembles of unitary random matrices relevant to the study of chaotic spectra in quantum mechanics. These are the circular orthogonal, unitary and symplectic ensembles, denoted COE, CUE and CSE respectively. For each of these three ensembles and their thinned versions, whereby each eigenvalue is deleted independently with probability $1 - \xi$, we take up the problem of calculating the first two terms in the scaled large $N$ expansion of the spacing distributions. It is well known that the leading term admits a characterisation in terms of both Fredholm determinants and Painlevé transcendents. We show that modifications of these characterisations also remain valid for the next to leading term, and that they provide schemes for high precision numerical computations. In the case of the CUE there is an application to the analysis of Odlyzko's data set for the Riemann zeros, and in that case some further statistics are similarly analysed."
N. Katz and P. Sarnak, Random Matrices, Frobenius Eigenvalues, and Monodromy (Colloquium Publications. American Mathematical Society, Vol 45, 1998)
[from the book's introduction:] "In a remarkable numerical experiment, Odlyzko found that the distribution of the (suitably normalized) spacings between successive zeroes of the Riemann zeta function is (empirically) the same as the so-called GUE measure, a certain probability measure on R arising in random matrix theory. His experiment was inspired by work of Montgomery, who determined the pair correlation distribution between zeroes (in a restricted range), and who noted the compatibility of what he found with the GUE prediction. Recent results of Rudnick and Sarnak are also compatible with the belief that the distribution of the spacings between zeros, not only of the Riemann zeta function, but also of quite general automorphic L-functions over Q, are all given by the GUE measure, or, as we shall say, all satisfy the Montgomery-Odlyzko Law. Unfortunately, proving this seems well beyond the range of existing techniques, and we have no results to offer in this direction.
However, it is a long established principle that problems which seem inaccessible in the number field case often have finite field analogues which are accessible. In this book we establish the Montgomery-Odlyzko Law for wide classes of zeta and L-functions over finite fields."
[from a book review:] "Mathematicians from Princeton University focus on the Montgomery-Odlyzko
law, the deep relation between the spacings between zeros of zeta and
L-functions and spacings between eigenvalues of random elements of
large compact classical groups. Finds the law to hold for wide classes of
zeta and L-functions over finite fields. Of interest to research
mathematicians and graduate students studying such areas as varieties over
finite and local fields, zeta-functions, limit theorems, and the structure of
families."
Z. Rudnick, "Zeta functions in arithmetic and their spectral statistics", Proceedings of a special semester at the Institut Poincaré, 1996.
[from introduction:] "The Riemann zeta function $\zeta(s)$ serves as an important model in many investigations into the theory of Quantum Chaos. My aims in these lectures, which are directed at physicists, are to explain some of the basic properties of $\zeta(s)$ used by number theorists, and discuss the spectral statistics of their zeros in connection with Random Matrix Theory."
Z. Rudnick
and P. Sarnak,
"Zeros of principal L-functions and
random matrix theory", Duke Mathematics Journal 81 (1996)
269-322 (special volume in honour of J. Nash).
E. Brezin, S. Hikami, "Characteristic polynomials of random matrices"
"Number theorists have studied extensively the connections between the distribution of zeros of the Riemann zeta-function, and of some generalizations, with the statistics of the eigenvalues of large random matrices. It is interesting to compare the average moments of these functions in an interval to their counterpart in random matrices, which are the expectation values of the characteristic polynomials of the matrix. It turns out that these expectation values are quite interesting."
E. Brezin, S. Hikami, "Logarithmic moments of characteristic polynomials of random matrices"
"In a recent article we have discussed the connections between averages
of powers of Riemann's zeta-function on the critical line, and averages
of characteristic polynomials of random matrices. The result for random
matrices was shown to be universal, i.e. independent of the specific probability
distribution, and the results were derived for arbitrary moments."
J.B. Conrey, M.O. Rubinstein, N.C. Snaith, "Moments of the derivative of the Riemann zeta-function and of characteristic polynomials" (AIM report no. 2005 - 20)
[abstract:] "We investigate the moments of the derivative, on the unit circle, of characteristic polynomials of random unitary matrices and use this to formulate a conjecture for the moments of the derivative of the Riemann zeta-function on the critical line. We do the same for the analogue of Hardy's Z-function, the characteristic polynomial multiplied by a suitable factor to make it real on the unit circle. Our formulae are expressed in terms of a determinant of a matrix whose entries involve the I-Bessel function and, alternately, by a combinatorial sum."
J.B. Conrey, D.W. Farmer, J.P. Keating, M.O. Rubinstein and N.C. Snaith, "Integral moments of L-functions"
[Abstract:] "We give a new heuristic for all of the main terms in the integral moments of various families of L-functions. The results agree with previous conjectures for the leading order terms. Our conjectures also have an almost identical form to exact expressions for the corresponding moments of the characteristic polynomials of either unitary, orthogonal, or symplectic matrices, where the moments are defined by the appropriate group averages. This lends support to the idea that arithmetical L-functions have a spectral interpretation, and that their value distributions can be modeled using Random Matrix Theory. Numerical examples show good agreement with our conjectures."
D. Farmer, F. Mezzadri, N.C. Snaith, "Random polynomials, random matrices, and L-functions, II" (preprint 09/05)
[abstract:] "We show that the Circular Orthogonal Ensemble of random matrices arises naturally from a family of random polynomials. This sheds light on the appearance of random matrix statistics in the zeros of the Riemann zeta-function."
[from introduction:] "This paper is motivated by the following questions: do the Riemann zeta-function and the other L-functions of number theory behave differently than random Dirichlet series with functional equation which just happen to satisfy the Riemann hypothesis? That is, does the Euler product have any effect on the zeros beyond forcing them onto the critical line? Our results suggest that the answer is 'yes', and the Euler product also has an effect on the local statistics of the zeros."
F. Mezzadri, "Random matrix theory and the zeros of zeta'(s)", J. Phys. A 36 (2003), 2945-2962 (Special Issue on RMT)
[abstract:] "We study the density of the roots of the derivative of the characteristic polynomial Z(U,z) of an N x N random unitary matrix with distribution given by Haar measure on the unitary group. Based on previous random matrix theory models of the Riemann zeta function zeta(s), this is expected to be an accurate description for the horizontal distribution of the zeros of zeta'(s) to the right of the critical line. We show that as N -> infinity the fraction of roots of Z'(U,z) that lie in the region 1-x/(N-1) <= |z| < 1 tends to a limit function. We derive asymptotic expressions for this function in the limits x -> infinity and x -> 0 and compare them with numerical experiments."
D.W. Farmer, "Mean values of the logarithmic derivative of the zeta function and the GUE hypothesis"
"The GUE Hypothesis, which concerns the distribution of zeros of the Riemann zeta-function, is used to evaluate some integrals involving the logarithmic derivative of the zeta-function. Some connections are shown between the GUE Hypothesis and other conjectures."
D.W. Farmer, "Modeling families of L-functions" (preprint 11/05)
[abstract:] "We discuss the idea of a 'family of L-functions' and describe various methods
which have been used to make predictions about L-function families. The methods involve a mixture
of random matrix theory and heuristics from number theory. Particular attention is paid to families of
elliptic curve L-functions. We describe two random matrix models for elliptic curve families:
the Independent Model and the Interaction Model."
O. Costin, J.L. Lebowitz, "Gaussian fluctuations in random matrices", Physical Review Letters, 75 (1995) 69.
"Let N(L) be the number of eigenvalues, in an interval of length L,
of a matrix chosen at random from the Gaussian Orthogonal, Unitary or
Symplectic ensembles of {\cal N} by {\cal N} matrices, in the limit
{\cal N}\rightarrow\infty. We prove that
[N(L) - \langle N(L)\rangle]/\sqrt{\log L} has a Gaussian distribution
when L\rightarrow\infty. This theorem, which requires control of all
the higher moments of the distribution, elucidates numerical and exact
results on chaotic quantum systems and on the statistics of zeros of
the Riemann zeta function."
C. Hughes, J. Keating, and N. O'Connell, "Random Matrix Theory and the Derivative of the Riemann Zeta Function", Proceedings of the Royal Society A456 (2000) 2611-2627.
"Random matrix theory (RMT) is used to model the asymptotics of the discrete moments of the derivative of the Riemann zeta function, $\zeta(s)$, evaluated at the complex zeros $\tfrac{1}{2}+\i\gamma_n$, using the methods introduced by Keating and Snaith. We also discuss the probability distribution of $\ln|\zeta'(1/2+\i\gamma_n)|$, proving the central limit theorem for the corresponding random matrix distribution and analysing its large deviations."
C. Hughes, "Central limit theorems and large deviations for the characteristic polynomial of a random unitary matrix and the Riemann zeta function" (a talk given at the DMV seminar "The Riemann zeta function and random matrix theory", Oct 2000)
C. Hughes, J. Keating, and N. O'Connell, "On the Characteristic Polynomial of a Random Unitary Matrix" (to be published in Communications in Mathematical Physics)
"We present a range of fluctuation and large deviations results for
the logarithm of the characteristic polynomial $Z$ of a random $N\times
N$ unitary matrix, as $N\to\infty$. First we show that
$\ln Z/\sqrt{\frac{1}{2}\ln N}$, evaluated at a finite set of distinct
points, is asymptotically a collection of i.i.d. complex normal random
variables. This leads to a refinement of a recent central limit theorem
due to Keating and Snaith, and also explains the covariance structure of
the eigenvalue counting function. We also obtain a central limit theorem
for $\ln Z$ in a Sobolev space of generalised functions on the unit
circle. In this limiting regime, lower-order terms which reflect the
global covariance structure are no longer negligable and feature in the
covariance structure of the limiting Gaussian measure. Large deviations
results for $\ln Z/A$, evaluated at a finite set of distinct points, can
be obtained for $\sqrt{\ln N} \ll A \ll \ln N$. For higher-order
scalings we obtain large deviations results for $\ln Z/A$ evaluated at a
single point. There is a phase transition at $A=\ln N$ (which only
applies to negative deviations of the real part) reflecting a switch
from global to local conspiracy."
G.A. Hiary, M.O. Rubinstein, "Uniform asymptotics of the coefficients of unitary moment polynomials" (preprint 05/2010)
[abstract:] "Keating and Snaith showed that the $2k^{th}$ absolute moment of the characteristic polynomial of a random unitary matrix evaluated on the unit circle is given by a polynomial of degree $k^2$. In this article, uniform asymptotics for the coefficients of that polynomial are derived, and a maximal coefficient is located. Some of the asymptotics are given in explicit form. Numerical data to support these calculations are presented. Some apparent connections between random matrix theory and the Riemann zeta function are discussed."
Y. Fyodorov, "Negative moments of characteristic polynomials of random matrices: Ingham-Siegel integral as an alternative to Hubbard-Stratonovich transformation", Nuclear Physics B 621 (2002) 643-674.
(Abstract) "We reconsider the problem of calculating arbitrary
negative integer moments of the (regularized) characteristic
polynomial for N x N random matrices taken from the Gaussian
Unitary Ensemble (GUE). A very compact and convenient integral
representation is found via the use of a matrix integral close to that
considered by Ingham and Siegel. We find the asymptotic expression
for the discussed moments in the limit of large N. The latter is of
interest because of a conjectured relation to properties of the
Riemann zeta-function zeroes. Our method reveals a striking
similarity between the structure of the negative and positive integer
moments which is usually obscured by the use of the
Hubbard-Stratonovich transformation. This sheds a new light on
"bosonic" versus "fermionic" replica trick and has some implications
for the supersymmetry method. We briefly discuss the case of the
chiral GUE model from that perspective."
Y.V. Fyodorov, G.A. Hiary and J.P. Keating, "Freezing transition, characteristic polynomials of random matrices, and the Riemann zeta-function" (preprint 02/2012)
[abstract:] "We argue that the freezing transition scenario, previously explored in the statistical mechanics of $1/f$-noise random energy models, also determines the value distribution of the maximum of the modulus of the characteristic polynomials of large $N \times N$ random unitary (CUE) matrices. We postulate that our results extend to the extreme values taken by the Riemann zeta-function $\zeta(s)$ over sections of the critical line $s=1/2+it$ of constant length and present the results of numerical computations in support. Our main purpose is to draw attention to possible connections between the statistical mechanics of random energy landscapes, random matrix theory, and the theory of the Riemann zeta function."
Yan V. Fyodorov and Jonathan P. Keating, Freezing transitions and extreme values: Random matrix theory, $\zeta(1/2+it)$, and disordered landscapes (preprint 11/2012)
[abstract:] "We argue that the freezing transition scenario, previously conjectured to occur in the statistical mechanics of $1/f$-noise random energy models, governs, after reinterpretation, the value distribution of the maximum of the modulus of the characteristic polynomials $p_N(\theta)$ of large $N\times N$ random unitary (CUE) matrices; i.e. the extreme value statistics of $p_N(\theta)$ when $N \rightarrow\infty$. In addition, we argue that it leads to multifractal-like behaviour in the total length $\mu_N(x)$ of the intervals in which $|p_N(\theta)|>N^x$, $x>0$, in the same limit. We speculate that our results extend to the large values taken by the Riemann zeta-function \zeta(s) over stretches of the critical line $s=1/2+it$ of given constant length, and present the results of numerical computations of the large values of $\zeta(1/2+it)$. Our main purpose is to draw attention to possible connections between extreme value problems in the statistical mechanics of $1/f$-noise random energy models, random matrix theory, and the theory of the Riemann zeta function, and to the potential consequences of freezing in the latter two cases."
Y.V. Fyodorov and P. Le Doussal, "Statistics of extremes in eigenvalue-counting staircases" (preprint 01/2020)
[abstract:] "We consider the number $\mathcal{N}(\theta)$ of eigenvalues $e^{i \theta_j}$ of a random unitary matrix, drawn from CUE$_{\beta}(N)$, in the interval $\theta_j \in [\theta_A,\theta]$. The deviations from its mean, $\mathcal{N}(\theta) - \mathbb{E}(\mathcal{N}(\theta))$, form a random process as function of $\theta$. We study the maximum of this process, by exploiting the mapping onto the statistical mechanics of log-correlated random landscapes. By using an extended Fisher–Hartwig conjecture, supplemented with the freezing duality conjecture for log-correlated fields, we obtain the cumulants of the distribution of that maximum for any $\beta >0$. It exhibits combined features of standard counting statistics of fermions (free for $\beta = 2$ and with Sutherland-type interaction for $\beta \ne 2$) in an interval and extremal statistics of the fractional Brownian motion with Hurst index $H=0$. The $\beta = 2$ results are expected to apply to the statistics of zeroes of the Riemann zeta function."
Z. Ahmed and S.R. Jain, "A pseudo-unitary ensemble of random matrices, PT-symmetry and the Riemann Hypothesis" (preprint 07/04)
[abstract:] "An ensemble of 2 x 2 pseudo-Hermitian random matrices is constructed that possesses real eigenvalues with level-spacing distribution exactly as for the Gaussian Unitary Ensemble found by Wigner. By a re-interpretation of Connes' spectral interpretation of the zeros of the Riemann zeta function, we propose to enlarge the scope of search of the Hamiltonian connected with the celebrated Riemann Hypothesis by suggesting that the Hamiltonian could also be PT-symmetric (or pseudo-Hermitian)."
Z. Ahmed, "Gaussian-random Ensembles of Pseudo-Hermitian Matrices", Invited Talk Delivered in 2nd International Workshop on 'Pseudo-Hermitian Hanmiltonians in Physics', Prague, June 14-16, 2004
[abstract:] "Attention has been brought to the possibility that statistical fluctuation properties of several complex spectra, or,
well-known number sequences may display strong signatures that the Hamiltonian yielding them as eigenvalues is PT-symmetric
(Pseudo-Hermitian). We find that the random matrix theory of pseudo-Hermitian Hamiltonians gives rise to new universalities of
level-spacing distributions other than those of GOE, GUE and GSE of Wigner and Dyson. We call the new proposals as Gaussian
Pseudo-Orthogonal Ensemble and Gaussian Pseudo-Unitary Ensemble. We are also led to speculate that the enigmatic
Riemann-zeros would rather correspond to some PT-symmetric (pseudo-Hermitian) Hamiltonian. "
R. Chhaibi, J. Najnudel and A. Nikeghbali, "The Circular Unitary Ensemble and the Riemann zeta function: The microscopic landscape" (preprint 10/2014)
[abstract:] "We show in this paper that after proper scalings, the characteristic polynomial of a random unitary matrix converges almost surely to a random analytic function whose zeros, which are on the real line, form a determinantal point process with sine kernel. Our scaling is performed at the so-called "microscopic" level, that is we consider the characteristic polynomial at points which are of order $1/n$ distant. We draw several consequences from our result. On the random matrix theory side, we obtain the limiting distribution for ratios of characteristic polynomials where the points are evaluated at points of the form $\exp(2i\pi\alpha/n)$. We also give an explicit expression for the (dependence) relation between two different values of the characteristic polynomial on the microscopic scale. On the number theory side, inspired by the Keating–Snaith philosophy, we conjecture some new limit theorems for the Riemann zeta function at the stochastic process level as well as some alternative approach to the conjecture by Goldston, Montgomery and Gonek for the moments of the logarithmic derivative of the Riemann zeta function. We prove our main random matrix theory result in the framework of virtual isometries to circumvent the fact that the rescaled characteristic polynomial does not even have a moment of order one, hence making the classical techniques of random matrix theory difficult to apply."
G.B. Arous, P. Bourgade, "Extreme gaps between eigenvalues of random matrices" (preprint 10/2010)
[abstract:] "This paper studies the extreme gaps between eigenvalues of random matrices. We give the joint limiting law of the smallest gaps for Haar-distributed unitary matrices and matrices from the Gaussian Unitary Ensemble. In particular, the $k$th smallest gap, normalized by a factor $n^{-4/3}$, has a limiting density proportional to $x^{3k-1}e^{-x^3}$. Concerning the largest gaps, normalized by $n/\sqrt{\log n}$, they converge in $\L^p$ to a constant for all $p>0$. These results are compared with the extreme gaps between zeros of the Riemann zeta function."
A. Edelman, P.-O. Persson, "Numerical methods for eigenvalue distributions of random matrices (preprint 01/05)
[abstract:] "We present efficient numerical techniques for calculation of eigenvalue distributions of
random matrices in the beta-ensembles. We compute histograms using direct simulations on very large matrices,
by using tridiagonal matrices with appropriate simplifications. The distributions are also obtained by
numerical solution of the Painleve II and V equations with high accuracy. For the spacings we show a technique
based on the Prolate matrix and Richardson extrapolation, and we compare the distributions with the zeros of
the Riemann zeta function."
P. Diaconis and M. Coram,
"New
Tests of the Correspondence Between Unitary Eigenvalues and the zeros
of Riemann's Zeta Function"
[PostScript]
T. Kriecherbauer, J. Marklof and A. Soshnikov,
"Random matrices and quantum chaos"
(brief introductory article, including a description of how this
relates to the Riemann Hypothesis)
J.-F. Burnol, speculative
excerpt from "On Fourier and zeta(s)"
relating the GUE hypothesis to his earlier work on physical interpretations
of number theoretical phenomena.
E. Wigner, "Random matrices in physics", SIAM Review 9
(1967) 1-123.
A.V. Andreev, O. Agam, B.D. Simons, B.L. Altschuler, "Quantum chaos,
irreversible classical dynamics, and random matrix theory", Physical Review
Letters 76 (1996) 3497
P. Deift, "Universality for mathematical and physical systems" (preprint 03/2006)
[abstract:] "All physical systems in equilibrium obey the laws of thermodynamics. In other words, whatever the precise
nature of the interaction between the atoms and molecules at the microscopic level, at the macroscopic level, physical
systems exhibit universal behavior in the sense that they are all governed by the same laws and formulae of thermodynamics.
In this paper we describe some recent history of universality ideas in physics starting with Wigner's model for the
scattering of neutrons off large nuclei and show how these ideas have led mathematicians to investigate universal behavior
for a variety of mathematical systems. This is true not only for systems which have a physical origin, but also for systems
which arise in a purely mathematical context such as the Riemann hypothesis, and a version of the card game solitaire
called patience sorting."
J.B. Conrey, D.W. Farmer, J.P. Keating, M.O. Rubinstein, N.C. Snaith, "Lower order terms in the full moment conjecture for the Riemann zeta function" (preprint 12/2006)
[abstract:] "We describe an algorithm for obtaining explicit expressions for lower terms for the conjectured full asymptotics of the
moments of the Riemann zeta function, and give two distinct methods for obtaining numerical values of these coefficients. We also provide
some numerical evidence in favour of the conjecture."
N.Kobayashi, M. Izumi, M. Katori, "Maximum distributions of noncolliding Bessel bridges" (preprint 08/2008)
[abstract:] "The one-dimensional Brownian motion starting from the origin at time $t=0$, conditioned to return to the origin at time $t=1$ and to stay positive during time
interval $0 < t < 1$, is called the Bessel bridge with duration 1. We consider the $N$-particle system of such Bessel bridges conditioned never to collide with each other in
$0 < t < 1$, which is the continuum limit of the vicious walk model in watermelon configuration with a wall. Distributions of maximum-values of paths attained in the time interval
$t \in (0,1)$ are studied to characterize the statistics of random patterns of the repulsive paths on the spatio-temporal plane. For the outermost path, the distribution function of
maximum value is exactly determined for general $N$. We show that the present $N$-path system of noncolliding Bessel bridges is realized as the positive-eigenvalue process
of the $2N \times 2N$ matrix-valued Brownian bridge in the symmetry class C. Using this fact computer simulations are performed and numerical results on the $N$-dependence
of the maximum-value distributions of the inner paths are reported. The present work demonstrates that the extreme-value problems of noncolliding paths are related with the
random matrix theory, representation theory of symmetry, and the number theory."
S. Torquato, A. Scardicchio, C.E. Zachary, "Point processes in arbitrary dimension from fermionic gases, random matrix theory, and number theory" (preprint 09/2008)
[abstract:] "It is well known that one can map certain properties of random matrices, fermionic gases, and zeros of the Riemann zeta function to a unique point process
on the real line. Here we analytically provide exact generalizations of such a point process in $d$-dimensional Euclidean space for any $d$, which are special cases of
determinantal processes. In particular, we obtain the $n$-particle correlation functions for any n, which completely specify the point processes. We also demonstrate that
spin-polarized fermionic systems have these same $n$-particle correlation functions in each dimension. The point processes for any $d$ are shown to be hyperuniform. The
latter result implies that the pair correlation function tends to unity for large pair distances with a decay rate that is controlled by the power law $r^{-(d+1)}$. We graphically
display one- and two-dimensional realizations of the point processes in order to vividly reveal their "repulsive" nature. Indeed, we show that the point processes can be
characterized by an effective "hard-core" diameter that grows like the square root of $d$. The nearest-neighbor distribution functions for these point processes are also
evaluated and rigorously bounded. Among other results, this analysis reveals that the probability of finding a large spherical cavity of radius $r$ in dimension $d$ behaves
like a Poisson point process but in dimension $d+1$ for large r and finite $d$. We also show that as $d$ increases, the point process behaves effectively like a sphere packing
with a coverage fraction of space that is no denser than $1/2^d$."
S. Tanaka, "Distribution of the Riemann zeros represented by the Fermi gas" (preprint 10/2010)
[abstract:] "The multiparticle density matrices for degenerate, ideal Fermi gas system in any dimension are calculated. The results are expressed as a determinant form, in which a correlation kernel plays a vital role. Interestingly, the correlation structure of one-dimensional Fermi gas system is essentially equivalent to that observed for the eigenvalue distribution of random unitary matrices, and thus to that conjectured for the distribution of the non-trivial zeros of the Riemann zeta function. Implications of the present findings are discussed briefly. "
S. Ali Altug, Sandro Bettin, Ian Petrow, Rishikesh and Ian Whitehead, "A recursion formula for moments of derivatives of random matrix polynomials" (preprint 12/2012)
[abstract:] "We give asymptotic formulae for random matrix averages of derivatives of characteristic polynomials over the groups $USp(2N)$, $SO(2N)$ and $O^-(2N)$. These averages are used to predict the asymptotic formulae for moments of derivatives of $L$-functions which arise in number theory. Each formula gives the leading constant of the asymptotic in terms of determinants of hypergeometric functions. We find a differential recurrence relation between these determinants which allows the rapid computation of the $(k+1)$st constant in terms of the $k$th and $(k-1)$st. This recurrence is reminiscent of a Toda lattice equation arising in the theory of $\tau$-functions associated with Painlevé differential equations."
C. Pineda and T. Prosen, "Non-universal level statistics in a chaotic quantum spin chain", Phys. Rev. E 76 (2007) 061127
[abstract:] "We study the level statistics of an interacting multi-qubit system, namely the kicked Ising spin chain, in the regime of quantum chaos. Long range quasi-energy level statistics show effects analogous to the ones observed in semi-classical systems due to the presence of classical periodic orbits, while short range level statistics display perfect statistical agreement with random matrix theory. Even though our system possesses no classical limit, our result suggest existence of an important non-universal system specific behavior at short time scale, which clearly goes beyond finite size effects in random matrix theory."
[author comment:] "[We attempt] to calculate the dimension of a Hilbert space associated with rotationally invariant systems of $n$ spins. The dimension was given in terms of the Möbius function."
J. Sakhr and J.M. Nieminen, "Local box-counting dimensions of discrete quantum eigenvalue spectra: Analytical connection to quantum spectral statistics" (preprint 11/2017)
[abstract:] "Two decades ago, Wang and Ong [Phys. Rev. A 55, 1522 (1997)] hypothesized that the local box-counting dimension of a discrete quantum spectrum should depend exclusively on the nearest-neighbor spacing distribution (NNSD) of the spectrum. In this paper, we validate their hypothesis by deriving an explicit formula for the local box-counting dimension of a countably-infinite discrete quantum spectrum. This formula expresses the local box-counting dimension of a spectrum in terms of single and double integrals of the NNSD of the spectrum. As applications, we derive an analytical formula for Poisson spectra and closed-form approximations to the local box-counting dimension for spectra having Gaussian orthogonal ensemble (GOE), Gaussian unitary ensemble (GUE), and Gaussian symplectic ensemble (GSE) spacing statistics. In the Poisson and GOE cases, we compare our theoretical formulas with the published numerical data of Wang and Ong and observe excellent agreement between their data and our theory. We also study numerically the local box-counting dimensions of the Riemann zeta function zeros and the alternate levels of GOE spectra, which are often used as numerical models of spectra possessing GUE and GSE spacing statistics, respectively. In each case, the corresponding theoretical formula is found to accurately describe the numerically-computed local box-counting dimension."
A. Chattopadhyay, P. Dutta, S. Dutta and D. Ghoshal, "Matrix model for Riemann zeta via its local factors" (preprint 07/2018)
[abstract:] "We propose the construction of an ensemble of unitary random matrices (UMM) for the Riemann zeta function. Our approach to this problem is 'piecemeal', in the sense that we consider each factor in the Euler product representation of the zeta function to first construct a UMM for each prime $p$. We are able to use its phase space description to write the partition function as the trace of an operator that acts on a subspace of square-integrable functions on the $p$-adic line. This suggests a Berry–Keating type Hamiltonian. We combine the data from all primes to propose a Hamiltonian and a matrix model for the Riemann zeta function."
S.C.L. Srivastava, A. Lakshminarayan, S. Tomsovic and A. Bäcker, "Ordered level spacing probability densities" (preprint 10/2018)
[abstract:] "Spectral statistics of quantum systems have been studied in detail using the nearest neighbour level spacings, which for generic chaotic systems follows random matrix theory predictions. In this work, the probability density of the closest neighbour and farther neighbour spacings from a given level are introduced. Analytical predictions are derived using a $3\times 3$ matrix model. The closest neighbour density is generalized to the $k$-th closest neighbour spacing density, which allows for investigating long-range correlations. For larger $k$ the probability density of $k$-th closest neighbour spacings is well described by a Gaussian. Using these $k$-th closest neighbour spacings we propose the ratio of the closest neighbour to the second closest neighbour as an alternative to the ratio of successive spacings. For a Poissonian spectrum the density of the ratio is flat, whereas for the three Gaussian ensembles repulsion at small values is found. The ordered spacing statistics and their ratio are numerically studied for the integrable circle billiard, the chaotic cardioid billiard, the standard map and the zeroes of the Riemann zeta function. Very good agreement with the predictions is found."
K. Blackwell, N. Borade, C. Devlin VI, N. Luntzlara, R. Ma, S.J. Miller, M. Wang and W. Xu, "Distribution of eigenvalues of random real symmetric block matrices" (preprint 08/2019)
"Random Matrix Theory (RMT) has successfully modeled diverse systems, from energy levels of heavy nuclei to zeros of $L$-functions. Many statistics in one can be interpreted in terms of quantities of the other; for example, zeros of $L$-functions correspond to eigenvalues of matrices, and values of $L$-functions to values of the characteristic polynomials. This correspondence has allowed RMT to successfully predict many number theory behaviors; however, there are some operations which to date have no RMT analogue. The motivation of this paper is to try and find an RMT equivalent to Rankin-Selberg convolution, which builds a new $L$-functions from an input pair.
For definiteness we concentrate on two specific families, the ensemble of palindromic real symmetric Toeplitz (PST) matrices and the ensemble of real symmetric (RS) matrices, whose limiting spectral measures are the Gaussian and semicircle distributions, respectively; these were chosen as they are the two extreme cases in terms of moment calculations. For a PST matrix $A$ and a RS matrix $B$, we construct an ensemble of random real symmetric block matrices whose first row is $\{A,B\}$ and whose second row is $\{B,A\}$. By Markov's Method of Moments, we show this ensemble converges weakly and almost surely to a new, universal distribution with a hybrid of Gaussian and semicircle behaviors. We extend this construction by considering an iterated concatenation of matrices from an arbitrary pair of random real symmetric sub-ensembles with different limiting spectral measures. We prove that finite iterations converge to new, universal distributions with hybrid behavior, and that infinite iterations converge to the limiting spectral measures of the component matrices."
T. Kimura, "A refinement of Sato–Tate conjecture" (preprint 01/2021)
[abstract:] "We propose a refined version of the Sato&ndah;Tate conjecture about the spacing distribution of the angle determined for each prime number. We also discuss its implications on $L$-function associated with elliptic curves in the relation to random matrix theory."
W.-J. Rao, "Higher-order level spacings in random matrix theory based on Wigner's conjecture" (preprint 05/2020)
[abstract:] "The distribution of higher order level spacings, i.e. the distribution of $\{s^{(n)}_i = E_{i+n} - E_i\}$ with $n\geq 1$ is derived analytically using a Wigner-like surmise for Gaussian ensembles of random matrix as well as Poisson ensemble. It is found $s^{(n)}$ in Gaussian ensembles follows a generalized Wigner–Dyson distribution with rescaled parameter $\alpha = \nu C^2_{n+1} + n - 1$, while that in Poisson ensemble follows a generalized semi-Poisson distribution with index $n$. Numerical evidences are provided through simulations of random spin systems as well as non-trivial zeros of Riemann zeta function. The higher order generalizations of gap ratios are also discussed."
Abstracts from MSRI conference "Random Matrices and Their Applications: Quantum Chaos, GUE Conjecture for Zeros of Zeta Functions, Combinatorics, and All That" (June 7-11, 1999)
MSRI archive - streaming video of numerous lectures on random matrix theory:
Random Matrix, Statistical Mechanics, and Integrable Systems Workshop, February 22-26, 1999
Random
Matrices and their Applications, June 7-11, 1999
Random Matrices Conference, MIT, 12 August 2001.
Zeta Functions, Random Matrices and Quantum Chaos Workshop, Bristol, UK, 13-14 September, 2001.
P.E. Cartier, B. Julia, P. Moussa and P. Vanhove (eds.), Frontiers in Number Theory, Physics, and Geometry: On Random Matrices, Zeta Functions, and Dynamical Systems (Springer, due March 2006)
[publisher's description:] "This book presents pedagogical contributions on selected topics relating Number Theory, Theoretical Physics and Geometry. The parts are composed of long self-contained pedagogical lectures followed by shorter contributions on specific subjects organized by theme. Most courses and short contributions go up to the recent developments in the fields; some of them follow their author's original viewpoints. There are contributions on Random Matrix Theory, Quantum Chaos, Non-commutative Geometry, Zeta functions, and Dynamical Systems. The chapters of this book are extended versions of lectures given at a meeting entitled Number Theory, Physics and Geometry, held at Les Houches in March 2003."
"Recent Perspectives in Random Matrix Theory and Number Theory", Isaac Newton Institute of Mathematical Sciences, Cambridge, UK, 29 March - 8 April 2004
This was linked with the Isaac Newton Institute programme:
"Random Matrix Approaches in Number Theory", 26 January - 16 July 2004
Workshop on Number Theory
and Random Matrix Theory, June 1-3, 2005, Waterloo, Canada
quantum mechanics page
archive tutorial mystery new search home contact