Beurling's generalised prime construction
chronological bibliography and notesE. Landau, "Neuer beweis des primzahlsatzes und beweis des primidealsatzes", Math. Ann. 56 (1903) 645-670.
A. Beurling, "Analyse de la loi asymptotique de la distribution des nombres premiers généralisés", Acta Math. 68 (1937) 255-291.
B. Nyman, "A general prime number theorem", Acta Math. 81, (1949) 299-307.
P. Malliavin, "Sur le reste de la loi asymptotique de répartition des nombres premiers généralisés de Beurling" Acta Math. 106 (1961) 281-298.
A. Beurling, "Construction and analysis of some convolution algebras", Annales de l'Institut Fourier, Grenoble 14 (1964) 1-32.
R.S. Hall, "Theorems about Beurling's generalised primes and the associated zeta function", Ph.D. Thesis, University of Illinois-Urbana, 1967
[abstract:] "Beurling defined a set, $P$, of generalized prime numbers as any non-decreasing unbounded
sequence of real numbers which are greater than one. The multiplicative semi-group, $N$, generated by the
elements of $P$ is called the associated set of generalized integers. The functions $Pi(x)$ and $N(x)$ are
defined, respectively, as the number of generalized prime and integers less than or equal to $x$. This paper
is concerned with deducing the behaviour of $Pi(x)$ from that of $N(x)$."
P.T. Bateman and H.G. Diamond, "Asymptotic distribution of Beurling's generalized prime numbers", Studies
in Number Theory, Mathematical Association of America Studies vol. 6
(W.J. Leveque, ed.), 1969, 152-210.
H.G. Diamond, "The prime number theorem for
Beurling's generalized numbers", Journal of Number Theory 1
(1969) 200-207.
H.G. Diamond, "Asymptotic distribution of
Beurling's generalized integers", Illinois Journal of Mathematics
14 (1970) 12-28.
H.G. Diamond, "A set of generalized numbers
showing Beurling's theorem to be sharp", Illinois Journal of
Mathematics 14 (1970) 29-34.
R.S. Hall, "The prime number theorem for generalized primes", Journal
of Number Theory 4 (1972) 313-320.
H.G. Diamond, "Chebyshev estimates for Beurling generalized prime
numbers", Proceedings of the American Mathematical Society 39
(1973) 503-508.
R.S. Hall, "Beurling generalized prime number systems in which the
Chebyshev inequalities fail", Proceedings of the American Mathematical
Society 40 (1973) 79-82.
C. Ryavec, "The analytic continuation of Euler products with
applications to asymptotic formulae", Illinois Journal of Mathematics
17 (1973) 608-618.
S. Segal, "Prime number
theorem analogues without primes", J. riene u. angew. Math. 265
(1974) 1-22.
H.G. Diamond, "Chebyshev type estimates in prime number theory", in
Seminaire de theorie des nombres, Universite de Bordeaux I, 1974-1975,
expose no. 24.
H.G. Diamond, "When do Beurling generalised integers have a density?", J. Reine
Angew. Math. 295 (1977) 22-39
H. Müller, "Über die asymptotische Verteilung von Beurlingschen Zahlen", J. Reine Angew. Math.
289 (1977) 181-187.
J.-P. Borel, "Quelques resultats d'equipartion lies aux nombres premiers
generalises de Beurling", Acta Arith. 38 (1980) 255-272
J.-P. Borel, "Sur le prolongement des fonctions zeta associees a un systeme
de nombres premiers generalises de Beurling", Acta Arith. 43 (1984) 273-282.
E. Stankus, "Analytic continuation of modified L-function",
Lithuanian Math. Journal 24 (1984) 176-181.
W.-B. Zhang, "Asymptotic distribution of Beurling's generalized prime numbers and integers",
Ph.D. Thesis, Univ. of Illinois, Urbana, 1986
Wen-Bin Zhang, "Chebyshev estimates for Beurling generalized prime
numbers", Proceedings of the American Mathematical Society
101 (1987) 205-212.
Wen-Bin Zhang, "A generalization of Halász's theorem to Beurling's generalised
integers and its application", Illinois J. Math. 31 (1987) 645-664
Wen-Bin Zhang, "Density and O-density of Beurling generalized integers",
Journal of Number Theory 30 (1988) 120-139.
Wen-Bin Zhang, "Chebyshev
type estimates for Beurling generalized prime numbers. II"., Trans. Am. Math. Soc. 337 (1993)
651-675
Sz. Revesz, "On Beurling's prime number theorem" Period. Math. Hungarica
28 (1994) 195-210.
E. Stankus, "On some generalized integers", Lithuanian Math. Journal,
36 (1996) 115-124.
J.-P. Kahane,
"A Fourier formula for prime numbers" Dedicated to
the memory of Carl Herz, Canadian Mathematical Society Conference
Proceedings 21 (1997) 89-102.
J.-P. Kahane, "Sur les nombres generalises de Beurling. Preuve
d'une conjecture de Bateman et Diamanond", Journal de Theorie des
Nombres Bordeaux 9 (1997) 251-266.
J.-P. Kahane, "Le role de l'algebre H1 de Sobolev dans la theorie
des nombres premiers generalises de Beurling", C.R. Acad. Sci. Paris
324 (1997) 251-266.
E. Stankus, "Modified zeta functions and the
number of g-integers", New Trends in Probability and
Statistics, Vol. 4 (Editors A. Laurincikas, et. al.) 247-258.
E.P. Balanzario, "An example in Beurling's
theory of primes", Acta Arithmetica 87 (1998) 121-139
J.-P. Kahane, "Le role des algebres A de Wiener,
 de Beurling et H1 de
Sobolev dans la theorie des nombres premiers generalises de
Beurling" Annales de l'Institut Fourier, Grenoble 48, 3
(1998) 611-648.
de Beurling et H1 de
Sobolev dans la theorie des nombres premiers generalises de
Beurling" Annales de l'Institut Fourier, Grenoble 48, 3
(1998) 611-648.
J.-P. Kahane, "Un theoreme de Littlewood pour les nombres premiers de
Beurling" Bulletin of the London Mathematical Society 31
(1999) 424-430.
M. Balazard, "La version
de Diamond de la methode de l'hyperbole de Dirichlet", L'Enseignement Math.
45 (1999) 253-270.
H. Montgomery, "Smooth
Beurling integers from irregular Beurling primes" (lecture presented at
University of Illinois, Urbana's Millennial Conference on Number Theory, May 21-26, 2000)
H.G. Diamond, H.L. Montgomery and U.M.A. Vorhauer, "Beurling primes with large oscillation", 334 (2006) 1-36
[abstract:] "A Beurling generalized number system is constructed having integer counting function $N_B(x)=\kappa x+O(x^\theta)$ with $\kappa>0$ and $1/2<\theta<1$, whose prime counting function satisfies the oscillation estimate $\pi_B(x)==li(x)+\Omega(x\exp(-c\sqrt{\log x}))$, and whose zeta function has infinitely many zeros on the curve $\sigma=1-a/\log t, t \geq 2$, and no zero to the right of this curve, where $a$ is chosen so that $a>(4/e)(1-\theta)$. The construction uses elements of classical analytic number theory and probability."
A.S. Fainleib, "On the distribution of Beurling integers", Journal of Number Theory 111 (2005) 227-247
[abstract:] "Asymptotic behaviour of the counting function of Beurling integers is deduced from Chebyshev upper bound and Mertens formula for Beurling primes. The proof based on some properties of corresponding zeta-function on the right of its abscissa of convergence."
T.W. Hilberdink, "Well-behaved Beurling primes and integers", Journal of Number Theory 112 (2005) 332-344
[abstract:] "In this paper, we study generalised prime systems for which both the prime and integer counting functions are asymptotically well-behaved, in the sense that they are approximately $li(x)$ and $\rho x$, respectively (where $\rho$ is a positive constant), with error terms of order $O(x^{\theta_1})$ and $O(x^{\theta_2})$ for some $\theta_1,\theta_2<1$. We show that it is impossible to have both $\theta_1$ and $\theta_2$ less than 1/2."
T.W. Hilberdink, "A lower bound for the Lindelöf function associated to generalized integers", Journal of Number Theory (in press)
Sz. Revesz, "Oscillation of the remainder term in the Beurling prime number formula" (presentation given at Rencontres de théorie analytique et élémentaire des nombres, Institut Henri Poincaré, 12/2006)
[abstract:] "Arne Beurling generalized the prime number theorem to the rather general situation when the role of primes are taken over by some arbitrary reals, and integers are simply the reals of the freely generated multiplicative subgroup of the primes given. If the "number of integers from $1$ to $x$" function takes the form $N(x) = x + O(x^a)$, with $a < 1$, then the corresponding Beurling zeta function has a meromorphic continuation to the half-plane to the right of $a$. Location of zeroes between the real part $= 1$ and real part = a lines are then crucial to the oscillation of the prime number formula, as is well-known in the classical case. The lecture describes how these relations can be established even in the generality of Beurling prime distribution."
W.-B. Zhang, "Beurling primes with RH and Beurling primes with large oscillation", Mathematische Annalen 337 (2007) 671-704
[abstract:] "Two Beurling generalized number systems, both with
$N(x)=kx+O(x^{1/2}}\exp\{c(\log\,x)^{2/3}\})$ and $k > 0$, are constructed. The associated zeta
function of the first satisfies the RH and its prime counting function satisfies $\pi(x) = li(x) + O(x^{1/2})$.
The associated zeta function of the second has infinitely many zeros on the curve $s = 1-1/log t$ and no zeros
to the right of the curve and the Chebyshev function $\psi(x)$ of its primes satisfies $\limsup\,
(\psi(x)-x)/(x\exp\{-2\sqrt{\log\,x}\})=2$ and $\liminf\, (\psi(x)-x)/(x\exp\{-2\sqrt{\log\,x}\})=-2$. A
sharpened form of the Diamond-Montgomery-Vorhauer random approximation and elements of analytic number theory
are used in the construction."
The only use of Beurling's generalisation by a physicist of which I am aware:
B. Julia, "Thermodynamic limit in number theory: Riemann-Beurling gases" Physica A 203 (1994) 425-436.
"We study the grand canonical version of a solved statistical model,
the Riemann gas: a collection of bosonic oscillators with energies the
logarithms of the prime numbers. The introduction of a chemical potential
$\mu$ amounts to multiply each prime by $e^{\mu}$, the
corresponding gases could be called Beurling gases because they are
defined by the choice of appropriate generalized primes when considered
as canonical ensembles; one finds generalized Hagedorn singularities in the
temperature. The discrete spectrum can be treated as continuous in its high
energy region; this approximation allows us to study the high energy level
density and is applied to Beurling gases. It is expected to be accurate for
the high temperature behaviour. One model (the logarithmic gases) will be
studied in more detail, it corresponds to the choice of all the integers strictly
larger than one as Beurling primes; we give an explicit formula for its grand
canonical thermodynamic potential $F - \mu N$ in terms of a
hypergeometric function and check the approximation on the Hagedorn
phenomenon. Related physical situations include string theories and quark
deconfinement where one needs a better understanding of the nature of the
Hagedorn transitions."
A set of Beurling generalised integers has the Delone property if the gaps between succesive members are bounded above and below. This was introduced by the Russian crystallographer and number theorist B.N. Delone in 1937, motivated by the question of whether the crystal-like nature of Z+ is relevant to the (presumed) truth of Riemann hypothesis, according to the following:
B.N. Delone, N.P. Dolbilin, M.I. Shtogrin, R.V. Galiulin, "A local criterion for regularity of a system of points", Sov. Math. Dok. 17 (1976) 319-322
This was brought to my attention by:
J. Lagarias, "Beurling generalized
integers with the Delone property", Forum Math. 11 (1999) 295-312
T.W. Hilberdink and M.L. Lapidus, "Beurling zeta functions, generalised primes, and fractal membranes" (preprint 08/04)

Here is an excerpt from the introductory section, which refers to Lapidus's emerging idea of a (noncommutative) flow of Beurling g-prime systems.


H. Delille, who in 2004 began making
and retracting claims that he had a proof of the Riemann hypothesis,
provided this summary of his work, which
involves the analytic continuation of Beurling zeta functions (August 2004).
In discussion with H. Diamond:
After seeing the original "prime evolution"
notes, Martin Huxley contacted me
to point out that I had re-invented the
basic idea of Beurling's construction. I
then contacted Harold Diamond who
appeared to be one of the leading experts in this field. Diamond examined
the notes and made the following comments:
"Prof. Huxley is correct: this topic lies in the area of Beurling generalized number theory. The essence of this theory is that if a sequence of g-integers is generated by a sequence of g-primes, and if one of the sequences is distributed sufficiently like its classical counterpart, then so too is the other."
"Equally spaced. I believe that the Riemann Hypothesis will not be settled until methods have been developed which make effective use of the equal spacing of integers. Note that the functional equation of the Riemann zeta function does have this information encoded into it."
I later asked him to elaborate on this intriguing prediction, and received the following reply:
"The functional equation of the Riemann zeta function does contain information about the equal spacing of the integers, but it is very subtle. It shows itself in a few ways:
1) If one requires only an asymptotic law for the integer counting function of the form N(x) = x + O(1), one could make examples in which the associated generalized zeta function

2) If you extend the 1/2 plane of convergence of the Riemann zeta function by the Euler-Maclaurin summation formula, the good spacing of the integers allows you to keep the process going ad infinitum.
3) If you extend the Riemann zeta function to the complex plane by use of the functional equation, the proofs of the functional equation all contain as an element the good spacing of the integers.
The reason for the claim that equal spacing of integers is likely to be essential for a proof of the Riemann hypothesis is this: there are quite simple Beurling-theory examples of nice counting functions N(x) for which such a good approximation as N(x) = x + O(1) exists, but for which the zeta function has zeros off the line Re s = 1/2. The examples have proper multiplicative structure, the log of the zeta function is of a suitable type, and there is good approximability of N(x) by x, but they lack additive structure."
[in reference to my speculations on the necessary conditions for g-integers to have asymptotic density 1:]
"There is quite a bit known about g-integers having asymptotic density 1. Roughly speaking, in addition to the g-primes having to be distributed rather like the usual ones, an additional condition is needed to cause the density be exactly 1.
A trivial remark: the set of generalized integers consisting of all odd numbers (the prime 2 has been killed) also has the property of being equally spaced. It says that the sequence of standard primes is not the only one that generates equally spaced integers. Note that in this example we have density 1/2.
Brief commments on my questions about modified zeta functions. First, this is very appropriate for studying such problems. Questions of half planes of convergence of the zeta function and behavior of the zeta function at the point 1 are easily answered in terms of the rate of growth of the integer counting function. Questions of an extension of the generalized zeta function to
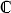 - {1} and its properties in the newly
gained territory appear to be
very difficult. It is not obvious how zeros of the zeta function
move around under perturbations of the primes. If you start with
the classical primes, and do your permutations one prime at a time,
you will not affect the classical zeta function zeros, but you will
induce a bunch of zeros and poles of the new zeta function on the
imaginary axis. If you are permuting everything at the same time,
I don't have a clue about the behavior of the zeros.
- {1} and its properties in the newly
gained territory appear to be
very difficult. It is not obvious how zeros of the zeta function
move around under perturbations of the primes. If you start with
the classical primes, and do your permutations one prime at a time,
you will not affect the classical zeta function zeros, but you will
induce a bunch of zeros and poles of the new zeta function on the
imaginary axis. If you are permuting everything at the same time,
I don't have a clue about the behavior of the zeros. Relating to my point about continuous prime distributions in section 3.6, in some sense Dirac measure at the point 1 + Lebesgue measure on
 represents another distinguished limiting
configuration that is related to the counting measure of positive
integers and is generated by a measure whose integral is close to
represents another distinguished limiting
configuration that is related to the counting measure of positive
integers and is generated by a measure whose integral is close to
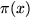 .
I have exploited this relation in several of my articles."
.
I have exploited this relation in several of my articles."I asked Professor Diamond to explain what he meant by "distinguished limiting configuration", and got the following reply:
"This is a bit queasy, but here goes.
Imagine that we set out to transmogrify the primes into a continuous mass distribution by successively cashing in classical primes and replacing them with a couple of nearby numbers, each with reduced multiplicity. For example, the factor (1 - 2-s)-1 in the product form of the Riemann zeta function could be replaced by a couple of factors of the form (1 - aj-s)-b_j for suitable numbers aj around 2 and suitable (small!) exponents bj. The notion of `suitable' is to keep the counting function N(x) pretty close to x. The process is repeated ad infinitum, at each stage causing each of the 'primes' to be replaced by a bunch of numbers each with much lower multiplicity. The distribution that I discussed, with counting measure Dirac measure at the point 1 + Lebesgue measure on
 has integral that is exactly
x, at
least for x > 1 and moreover, the associated zeta function has a logarithm which is very
analogous to the log of the Riemann zeta function.
has integral that is exactly
x, at
least for x > 1 and moreover, the associated zeta function has a logarithm which is very
analogous to the log of the Riemann zeta function.I have written about this stuff in some of the Beurling articles."
archive tutorial mystery new search home contact