 'prime evolution' notes[third version - 27/08/04]If you were not one of the recipients of the original announcement e-mailed on 23/11/99, then it's probably a good idea to read this explanation first. If you've already seen a version of this page, you may be interested in
a new development which appears to put the main
idea (1.5 below) in an entirely new light.
original version of these notes (23/11/99) second version of these notes (23/11/99) - almost identical to this document Warning: The contents of this document are somewhat vague. This is an unavoidable consequence of (1) the unorthodox nature of the material and (2) my relative unfamiliarity with some of the technical issues involved and general reliance on intuition. Rather than approaching this as a coherent whole, I suggest you see it as a loose collection of curious notions, amongst which there may be one or two useful new ideas. If you wish to demonstrate that this is all nonsense (and you may be right - I just don't know), then you are invited to explain why for the benefit of myself and others. Note: When I discovered this extraordinary preprint in April 2001, I sensed that it might provide a certain framework within which to meaningfully reformulate my speculations: I.V. Volovich, "Number theory as the ultimate physical
theory", p-Adic Numbers, Ultrametric Analysis and Applications 2 (2010) 77–87 Table of Contents1. 'Arithmetic dynamics' and Beurling's generalised prime construction 2. Generalised zeta functions 3. More dynamics (quantisation, etc.) 4. 1/f noise and self-organising criticality 5. Partition functions and probability densities 6. Random matrix theory (the Gaussian Unitary Ensemble) 7. General mathematical considerations 8. General physics considerations 9. Other ideas for dynamics 10. Miscellaneous questions References 1. 'Arithmetic dynamics' and Beurling's generalised prime construction
One might guess that the primes are unique in
this way, but this is not the case. For if we remove 2 from the sequence of
primes to give
For example, we know when P(x) ~ x/log x (the prime number theorem), and N(x) is just the simple unit-step function [x]. One obvious question concerns the extent to which we can deform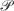 without
affecting the property N(x) ~ 1. In other words, when
does a sequence without
affecting the property N(x) ~ 1. In other words, when
does a sequence 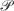 generate a
multiplicative semigroup with 'asymptotic density' = 1? generate a
multiplicative semigroup with 'asymptotic density' = 1?
The essence of the theory is that if a sequence of g-integers is generated by a sequence of g-primes, and if one of the sequences is distributed sufficiently like its classical counterpart, then so too is the other. To be more precise, Beurling proved Theorem: If N(x) satisfies the asymptotic relation N(x) = Ax + O(x/logcx) for some A > 0 and c > 3/2, then the
conclusion of the prime number theorem is valid for the system of g-primes
P(x) ~ x/log x. A comprehensive bibliography and set of notes concerning the Beurling construction can be found here.
The idea is that the sequence
of primes represents a 'balanced' or 'equilibrium' state, an 'attractor'
where the forces responsible for the evolution vanish. Through a process of
self-organisation or feedback, a sequence could conceivably evolve towards
'primeness' and stop when it reaches this state (where each
pj(t) = pj, the jth prime).
We can think of
'primeness' in this situation as a kind of 'arithmetic equilibrium' where
addition and multiplication are in harmony with each other, characterised
by the geometric regularity of the multiplicative semigroup
[This idea preceded my awareness of Beurling's work. Many thanks to M. Huxley for bringing it to my attention after seeing the original version of these notes]
"...the chemical potential I introduced in my 1989 lecture and discussed further in Strasbourg Dec. 1983 paper and Physica A 1994 article (with Beurling in the title) had actually been introduced by Sathe and Selberg before. This parameter gives a flow in the space of Beurling theories. I first mentioned Beurling gases in a talk at ENS Summer institute before Strasbourg. Since about 4 years [ago] I am really thinking in terms of evolution too, I should look at your notes to see if there is any overlap there. I was indeed rather busy unfortunately." The 1994 article in question is: B. Julia, "Thermodynamic limit in number theory: Riemann-Beurling gases" Physica A 203 (1994) 425-436. Having looked at this, I've not found any obvious overlap with my ideas here. However, I'd be interested to know what precisely Julia is refering to when he says "the space of Beurling theories". For some time I've been wondering what kind of space would be the appropriate setting for the 'evolution' of sequences described in 1.5.
T.W. Hilberdink and M.L. Lapidus, "Beurling zeta functions, generalised primes, and fractal membranes" (preprint 08/04)
The following excerpt from the introductory section refers to Lapidus's forthcoming book In Search of the Riemann Zeros, and the fact that it will include a new body of ideas associated with a "continuous-time 'dynamical deformation' of Beurling zeta functions and prime systems [which] would provide a new away to understand the remarkable role played (within the broader class of Beurling-type zeta functions) by arithmetic (or number-theoretic) zeta functions, such as the Riemann zeta function..."
The charge on a particle/g-prime pj(t)
would perhaps be given by an
infinite sum of weighted contributions from each of its multiples in
Beurling was trying demonstrate the 'sharpness' of his central theorem by
constructing an example of a system
N(x) = Ax + O(x/logcx) is satisfied by the associated g-integers for A > 0 and c = 3/2, but the g-primes fail to satisfy the 'prime number theorem' relation P(x) ~ x/log x. Recall from 1.4 that this relation is necessarily satisfied when c > 3/2.He succeeded in doing this, but chose to use a continuous analogue of a g-prime system. His example involved a continuous 'prime measure' and associated 'integer measure', which differ from the usual (atomic) counting measures of prime number theory. In a 1970 article, H. Diamond produced a conventional system of (atomic) g-primes with the required property, thereby showing that the use of continuous g-prime measures is not necessary to demonstrate that Beurling's theorem [1.4] is sharp. In a personal communication (21/09/00) Diamond stated "The reason that Beurling used the continuous measures rather than atomic measures is that they are simpler and more natural than the others. He was such a good mathematician, that I am sure that if he had wanted to make a discrete example, he certainly could have done so. My discrete example was in fact based on Beurling's example. Roughly speaking, my prime counting function is [ ] of Beurling's counting function, where [ ] is the greatest integer function." Continous g-prime measures appear again in Diamond's 1969 article. The idea is to replace the counting functions P(x) and N(x) with more general functions which need not be unit-step functions, and which can even be continous. Diamond introduces increasing functions N(x) and
 is not the
generalisation of the usual g-prime counting function
P(x). Rather, it generalises
P(x) + 1/2 P(x1/2) +
1/3 P(x1/3) + ..., which counts g-primes
and their powers, with inverse-power weight, a
phenomenon familiar from the theory of the classical prime distribution. is not the
generalisation of the usual g-prime counting function
P(x). Rather, it generalises
P(x) + 1/2 P(x1/2) +
1/3 P(x1/3) + ..., which counts g-primes
and their powers, with inverse-power weight, a
phenomenon familiar from the theory of the classical prime distribution.
This suggests the possibility of an evolving continuous (rather than discrete) system of g-primes resulting, via some deterministic feedback or self-organisation process, in the classical prime distribution. This animation, although not directly related, has some suggestive value here: We see the gradual emergence of the classical primes as pointlike objects
from a continuum, here based on the nontrivial zeros of
the Riemann zeta function [thanks to Raymond Manzoni for this animation]
P(x) ~ x/log x by which the classical primes distribute.M. Wolf has discovered the presence of 1/f noise in the classical prime distribution. This is a property of power-frequency spectra, and has been shown to be closely related to the phenomenon of self-organised criticality by Bak, Tang and Wiesenfeld. Wolf has shown that the 1/f noise is due to the logarithmic distribution
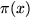 is due only to the residue contribution
of the simple pole at
s = 1. The effect of the nontrivial zeros of the zeta function
(which govern the local fluctuations) are not taken into account.
We will return to these matters in section 4. is due only to the residue contribution
of the simple pole at
s = 1. The effect of the nontrivial zeros of the zeta function
(which govern the local fluctuations) are not taken into account.
We will return to these matters in section 4.
2. Generalised zeta functions
to arrive at the idea of 'modified zeta functions', which evolve continuously with a continuously evolving sequence of particles (system of g-primes). These generalisations of Riemann's zeta function have been studied in the theory surrounding Beurling's g-prime construction.
which relates the set of classical primes to its multiplicative semigroup,
A few questions come to mind (H. Diamond's response to these can be found here):
2.3 For which sequences
2.4 For which of these sequences will the corresponding
g-zeta functions allow analytic continuation to 2.5 For which of these sequences will the (analytic continuations of the) g-zeta functions have simple poles at s= 1? 2.6 For which of these sequences will the corresponding zeta functions produce sets of 'trivial' zeros on the negative real axis? Sets of 'nontrivial' zeros contained within the critical strip 0 <Re s < 1 ? 'Nontrivial' zeros symmetric with respect to the critical line Re s = 1/2 ? 2.7 For which of these sequences will the corresponding g-zeta functions produce sets of nontrivial zeros with GUE-like spacing statistics ? (The usual zeta function has this property. GUE = Gaussian Unitary Ensemble.)
2.8 Consider how the prime-counting step function
Under what conditions can we guarantee that the analogous limit function, built from powers of x where the exponents are the zeros of the g-zeta function, will coincide with P(x)? Equivalently we can ask which systems of g-primes have valid 'explicit formulae' analogous to those of Riemann and von Mangoldt.
Suppose the Hilbert-Polya conjecture is
correct, and the complex zeros of the usual zeta function do
replicate the spectrum of eigenvalues of a Hermitean operator on a Hilbert
space. We might then consider in what ways we can modify the classical primes
so that the resulting sets of zeros in 3. More dynamics (quantisation, etc.)
System of g-primes evolves Can this be made meaningful? If so could it be in some way compatible with the arithmetic dynamics suggested in Section 1?
H. Diamond's comments on continuous prime distributions can be found here.
where R is the
the function introduced by Riemann to approximate Could this identity be related to a dynamical law which holds throughout the evolutionary process? The prime fluctuation function D(x) =
It would seem that the base states are going to relate somehow to the various rescalings of R, or 'prime harmonics'.
A graph of the prime density fluctuation function D(x) from[GHR]. This seemingly 'noisy signal' can be decomposed into 'harmonics' corresponding directly to the zeta zeros. Michael Berry and others have often used musical analogies.
However, the arithmetic dynamics need not be conservative. In [GHR], the authors calculate the four Liapunov exponents of the prime density fluctuation function, arriving at a sum of -0.07. As there is a margin of error involved, and this sum is reasonably close to zero, the authors safely conclude that the "unknown dynamical system" associated with the prime distribution could be either conservative or dissipative. Note that the authors were approaching the prime distribution from the point-of-view of interested chaos theorists. They applied a technique to the primes which is normally applied by physicists to experimental data generated by a (possibly unknown) dynamical system, to determine if it is chaotic, etc. It seems that they were not (consciously) suggesting that the primes are the result of some dynamical evolution, as I am here. 4. 1/f noise and self-organising criticality
This suggests something like a 'surface' L of similarly distributed systems of g-primes (in whichever space we are using).
The sandpile dynamics might have to be adapted so that 'continua' rather than 'quanta' of sand flowed from one position to its neighbours, and so that the mechanism governing this was probabilistic rather than deterministic. In this way, the 1-dim. sandpile would be seen to gradually 'level itself out' or approach equilibrium, corresponding to a system of g-primes on the surface L. The 'arithmetic' forces might then be responsible for the finer points of the distribution.
This brought to mind the curious quotation from J.J. Sylvester: "I have sometimes thought that the profound mystery which envelops our conceptions relative to prime numbers depends upon the limitations of our faculties in regard to time, which like space may be in essence poly-dimensional and that this and such sort of truths would become self-evident to a being whose mode of perception is according to superficially as opposed to our own limitation to linearly extended time." from Collected Mathematical Papers, Volume 4, page 600 which in modern English says something like: "I have sometimes thought that the distribution of prime numbers only seems mysterious to us because of our limitations in perception related to time. Time, like space, may be multi-dimensional, and perhaps to a being who could perceive a more generalised kind of time there would be no mystery surrounding prime numbers - it would all be obvious."
With the utmost respect to Professor Berry, I feel that he might be overlooking the point of what Wolf has discovered. I can see the value of rescaling spectra of energy levels, etc. and studying their statistics. looking at the statistics of the rescaled nontrivial zeta zeros has proven similarly rewarding, and as he points out here, the very structure of the prime distribution suggests rescaling. But why dismiss a potentially crucial result due to a "failure to rescale"? The primes, in their natural state, show a very particular kind of logarithmic density, which is mathematically linked to the remarkable and ubiquitous phenomenon of 1/f noise. This may be coincidental, but it's at least worth considering, especially with all of the emerging, and largely mysterious links between primes and various aspects of modern physics.
Although this involves a couple of speculative leaps, we could imagine that some kind of self-organisation process is responsible for bringing about the asymptotic 'equal spacing' in the evolving g-integers. The exact equal spacing of Recall from 1.12 that if we go back to the
explicit formula of Riemann and von Mangoldt, we see that the
approximation x/log x for
5. Partition functions and probability densities
Recall that the partition function is the fundamental object of study for a
system in thermodynamics, much as
Although it is not clear to me what these probabilities ultimately refer to in the context of [J], I suspect that they might be involved in what I'm trying to achieve.
Equivalently, we can consider the individual function pn(x)=1/( Again, it's not clear what the 'occurring' means here. Julia seems to be ambiguous on this point (or there is some subtlety I have missed). To understand what these probabilities actually refer to, I believe we really need a number theoretic understanding of 'temperature' in this context, as they are T -dependent. The partition function of a system is conventionally derived from certain basic assumptions of thermodynamic theory. Trying to adapt the same derivation to the (number theoretic) free Riemann gas in order to fully understand it would be very helpful here. We find that the locations of the maxima mn (n >
1) of the functions pn tend slowly towards 1 as n m2= 1.8791006..., m3 = 1.6351665..., m4 = 1.5329592..., m5 = 1.4743970... m10 = 1.3740486..., m20 = 1.3696203..., m30 = 1.3692338..., m40 = 1.3690822... The areas under these curves are finite, so we could normalise and
arrive at a sequence of probability densities, one for each n over
the interval If these probabilities are saying anything, it is (loosely speaking) this: In some unknown context, n = 1 is certain to 'occur' at absolute zero temperature (T = 0, so x is infinite), and all other natural numbers n are most likely to 'occur' near 1, with larger numbers tending to 'occur' closer and closer to 1. Note that as x
Also note that generalised zeta functions of Section 2 will produce modifications of the 'Julia partitions' for each x. Hence the individual probability functions pn(x) described above could be seen as evolving.
6. Random matrix theory (the Gaussian Unitary Ensemble)
One blatant similarity is the following pairwise correlation function which applies in both settings:
Here g(r) is the probability that you will find another eigenvalue (zero) a distance r away from a given eigenvalue (zero). This formula had been discovered in the context of random matrix theory by Freeman Dyson, and separately for zeta zero statistics by Hugh Montgomery. They coincidentally became aware of the similarity in each others' work in 1972 while talking informally over tea at Princeton where Montgomery was a visitor. A graph of g(x) looks like this:
It is often said that this suggests a 'repulsion' between zeros, unlike the Poisson spacing statistics. If we imagine that the distribution of primes is the result of an evolutionary process, then the zeta zeros will be the result of an accompanying 'dual' evolution (see Section 2). Could this 'repulsion' evident in the 'final state' of the zeta zeros'evolution somehow reflect a repulsive tendency within the evolutionary dynamics suggested in section 1 (and/or its dual)?
The statistics discussed in 6.1 relate to the behaviour of eigenvalues of matrices taken at random from this ensemble. It is not difficult to make precise and meaningful statements about this. Now if it exists, the hypothetical Hilbert-Polya operator is one fixed operator, it cannot be 'random', yet it is often said that it behaves like an (arbitrarily large) random unitary matrix. Such statements are based on the remarkable correspondence of statistical properties discussed above. To me, this suggests that the statistics of the zeta zeros might be an indication of some kind of (evolutionary) 'history' associated with the zeta function, and the related Hilbert-Polya operator. For the connection with the GUE suggests an entire class of operators, and that the operator we're looking for has taken other 'values' in the 'past'. The GUE probability density could then be a clue as to the actual dynamics governing the evolution. It seems to suggest that the evolving Hermitean operator is more likely to take some values than others, in a very particular way. However, this view may be entirely misguided. These comments from [BK] (p.245) may help to clarify: "It is important to note that we are here considering individual systems
and not ensembles, so statistics cannot be defined in the usual way, as
ensemble averages. Instead, we rely on the presence of an asymptotic
parameter: high in the spectrum (or for large t in the Riemann case),
there are many levels (or zeros) in a range where there is no secular variation,
and it is this large number that enables averages to be performed.
Universality then emerges in the limit h-bar A mathematical theory of universal spectral fluctuations already exists in the more conventional context where statistics are defined by averaging over an ensemble. This is random-matrix theory, where the correlations between matrix eigenvalues are calculated by averaging over ensembles of matrices whose elements are randomly distributed, in the limit where the dimension of the matrices tends ot infinity. Here the relevant ensemble is that of complex hermitean matrices: the "Gaussian unitary ensemble" (GUE). As will be discussed in the next section, it is precisely these statistics that apply to high eigenvalues of individual chaotic systems without time-reversal symmetry, and also to high Riemann zeros, in the sense that the spectral or Riemann-zero averages described in the previous paragraph coincide with GUE averages." 7. General mathematical considerations
which could be then be expressed in terms of cosh and sinh. This suggests that Dirichlet series are in some sense analogous to Fourier series, but concerned with periodicities on a logarithmic scale (i.e. self-similarity). I had wondered if an analogous 'Dirichlet analysis' had been developed. Julia pointed out to me recently that this is all made explicit in Hardy and Wright's book [HW]. Note that (1) the Riemann zeta function Also note that Marek Wolf has discovered at least three different kinds of self-similarity within the distribution of primes.
It may also be of some interest to note that the graph of y = log x is one of the simplest self-similar objects which can be constructed. Its self-similarity is evident when you rescale the x-axis, and the graph simply 'scrolls' up or down parallel to the y-axis.
8. General physics considerations
Also, Wolf and Julia have pointed out that the Kramers-Wannier duality [KW], which relates to Ising models and lattice gases, is strongly analogous to the functional equation of the Riemann zeta function.
As discussed in [BK] random matrices are linked
to the primes through the GUE spacing statistics of the nontrivial zeros of
the Riemann zeta function. This is absolutely central to the
'spectral interpretation'
approach to the Riemann hypothesis.
Is this 'triangle of relationship' fully understood? Could Brownian motion have some role to play in the evolutionary dynamics? After discovering the paper "Ladder heights, Gaussian random walks, and the Riemann zeta function" by the statisticians J. Chang and Y. Peres, which involves issues related to Brownian motion, I contacted Professor Peres and asked: "Preumably you are aware of the connections between random matrix theory (particularly the Gaussian Unitary Ensemble) and the spectral interpretation of the Riemann zeta function. It seems quite plausible that what you have done may be related. I seem to recall that Dyson demonstrated a relationship between random matrix theory and Brownian motion. Any thoughts on this?" He replied: "I am aware of the classical relations you mention, but not of any explicit connection of them to our work. It would be great to find such a connection. Another relevant survey paper by Biane, Pitman and Yor is attached." 9. Other ideas for dynamics
Intuition suggests that the immediate obstacles to giving this a coherent mathematical description might be overcome through the application of non-standard analysis. Note that this 'starting point' doesn't technically correspond to a system of g-primes, as the sequence of particles is not unbounded.
10. Miscellaneous questions
References[BK] M. Berry and J. Keating, "The Riemann zeros and eigenvalue asymptotics", SIAM Review 41, no. 2 (1999) 236-266. [W] M. Wolf, "1/f noise in the distribution of prime numbers", Physica A, 241 (1997) 493-499. [GHR] Z.Gamba, J.Hernando and L.Romanelli, "Are the prime numbers regularly ordered?", Physics Letters A 145, no.2,3 (1990) 106-108. [HW] G.H. Hardy and E.M. Wright, An Introduction to the Theory of Numbers, Clarendon Press, Oxford (1945) [BTW] P.Bak, C. Tang and K. Wiesenfeld ,"Self-organized criticality", Physical Review A, 38, no.1 (1988) 364-374. [J] B. Julia, "Statistical theory of numbers" from Number Theory and Physics (Springer Proceedings in Physics, Volume 47. editors Luck, Moussa and Waldschmidt, 1990) [J2] B. Julia, "Thermodynamic limit in number theory: Riemann-Beurling gases", Physica A 203 (1994) 425-436. [BC] J.-B. Bost and A. Connes "Hecke Algebras, Type III factors and phase transitions with spontaneous symmetry breaking in number theory," Selecta Mathematica (New Series), 1 (1995) 411-457. [HL] D. Harari and E. Leichtnam, "Extension du phenomene de brisure spontanee de symetrie de Bost-Connes au cas des corps globaux quelconques," Selecta Mathematica, (New Series), 3 (1997) 205-243. [C] P. Cohen "Dedekind zeta functions and quantum statistical mechanics" (ESI preprint). [LY] T. Lee and C.Yang, "Statistical theory of equations of state and phase transitions", Physical Review, 87, no.3 (1952) 404-419. [KW] H.A.Kramer and G.H.Wanier, "Statistics of the two-dimensional ferromagnet. Part I", Physical Review 60 (1941) 252-. [O] A. Odlyzko, "Primes, quantum chaos, and computers" [GR] L. Greengard and V. Rokhlin, "A fast algorithm for particle simulations", Journal of Computational Physics, 73 (1987) 325-348. [D] F.J. Dyson, "A Brownian-motion model for the eigenvalues of a random matrix", Journal of Mathematical Physics, 3 (1962), 1191-1198. [B] P. Billingsley, "Prime numbers and Brownian motion", American Mathematical Monthly, 80 (1973) 1099-1115. [BK] M.V. Berry and J.P. Keating, "The Riemann zeros and eigenvalue asymptotics", SIAM Review, 41, No.2 (1999), 236-266. [GP] H.Gopalkrishna Gadiyar and
R.Padma, "Ramanujan-Fourier series, the
Wiener-Khintchine formula and the distribution of prime pairs",
Physica A 269 (1999) 503-510.
number theory and physics archive number theory and time (link added 28/05/04) number theory, time and ancient Chinese aesthetics (link added 28/05/04) home contact |
 denote the multiplicative semigroup generated by
denote the multiplicative semigroup generated by  are equally spaced.
are equally spaced.



 might possibly
correspond to some kind of singularity in the field in which the particles
are moving. However, as
might possibly
correspond to some kind of singularity in the field in which the particles
are moving. However, as  and connected by the relation
and connected by the relation

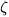 . The image
of stars condensing out of clouds of gas comes to mind. Although the
animation suggests a continuous mathematical process, it is based on
a set of discrete steps, one for each pair of nontrivial zeros. There are a
number of ways we could transform this into a continuous process
('blurring out' the zeros of
. The image
of stars condensing out of clouds of gas comes to mind. Although the
animation suggests a continuous mathematical process, it is based on
a set of discrete steps, one for each pair of nontrivial zeros. There are a
number of ways we could transform this into a continuous process
('blurring out' the zeros of 
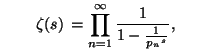
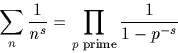
 , like the usual
Riemann zeta function?
, like the usual
Riemann zeta function?
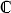 \ {1}?
\ {1}?
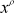 where the
where the  are the zeros of the usual Riemann
zeta function. Suppose then that we 'perturb' the classical primes slightly to
produce a system of g-primes
are the zeros of the usual Riemann
zeta function. Suppose then that we 'perturb' the classical primes slightly to
produce a system of g-primes  g-zeta function
evolves
g-zeta function
evolves  .
.
 are to behave like eigenvalues, we might
consider what the corresponding eigenstates (base states) could be.
Consider the expansion
are to behave like eigenvalues, we might
consider what the corresponding eigenstates (base states) could be.
Consider the expansion
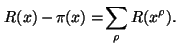



 nx) = probability of n
'occurring' at (inverse 'temperature') x.
nx) = probability of n
'occurring' at (inverse 'temperature') x.
 .
Some examples:
.
Some examples:

 an /n
x =
an /n
x =  onto the real line in such a
way that the multiplicative identity 1 gets mapped to the additive
identity 0. The reason that the primes are logarithmically 'spaced out'
would appear to be closely linked to the fact that the domain in which
they exist has an edge (i.e. they live in a half-continuum).
onto the real line in such a
way that the multiplicative identity 1 gets mapped to the additive
identity 0. The reason that the primes are logarithmically 'spaced out'
would appear to be closely linked to the fact that the domain in which
they exist has an edge (i.e. they live in a half-continuum).
 +?
+?
 + rather than towards
+ rather than towards
 as describing 'force fields' in
as describing 'force fields' in
 .
.