The above results about resonant drift were for external
perturbations modelled as an additional current in the equation for the
transmembrane potential, with an explicit time dependence. This is
easy for numerical simulation, but does not correspond to real
situation, where the defibrillating voltage current is not applied
across the membrane, but imposed extracellularly. Therefore, the above
results are not directly comparable to experimental data. Specifically,
this concerns the values of amplitudes of the stimuli, measured in
or 
, which have little and indirect relation to
experimental values of 
or 
. This is not a matter of
mere rescaling, by estimating how much of the external current actually
penetrates the cell membrane, but is a more fundamental difference in
biophysical mechanisms of action of this current onto the cell, since
the same current will cross the membrane of the same cell at the same
time in different directions in different parts of the membrane, and
thus will always have both depolarising and hyperpolarising actions on
the cell as a
whole. So, the amplitudes of the above numerical results may be interpreted, at
most, only qualitatively and in units relative to something that is
also experimentally measurable, e.g. defibrillation threshold (DFT).
An absolute quantitative estimation of DFT can be obtained by a quantitative theory of the interaction of extracellular current with membrane excitation processes (see e.g. [34]) with a theory of defibrillation [35, 36, 37]. This has been applied to the OGPV model in [38], and has led to the estimation which is, at least in the order of magnitude, comparable to experimental values. The basic idea of the description is that if the external current comes in through a part of the cell membrane in one direction, exactly the same current must come out through another part of the membrane. The resulting model can be written in the form
where the notations are mainly the same as in (1), (2),
with the difference that V and 
are average values over the
cell, 
external current flowing through the cell, 
effective cell conductivity with respect to this current, and 
are two vectors of faster
gating variables, which behave significantly differently in the two
membrane parts (these include `h', `d' and `f').
The physical meaning of and is that
is additional transmembrane voltage produced
by external current, which roughly corresponds to the external electric
field magnitude times typical size of the cell. More accurate
relationship with the external field requires solution of an elliptic
problem depending on the cell geometry, external field direction and
conductivity of intra- and extracellular liquids.
The gating variables
` 
' were not dynamic variables but fixed functions of
the transmembrane voltages 
. All the
dynamic quantities V, , and are
functions of time and of the location of the cell in space;
has been considered as a function of time only, i.e. it was
assumed that the current is uniform over the tissue.
The validity of this simple system of equations depends on several assumptions, including the separation of time scale of various processes and approximation of the cell body by just two compartments; these were verified by numerical tests in [38].
Typical responses of a spiral wave in this model to a 
pulse of
are shown on figs. 10 and 11. The
stimulus has both depolarising and repolarising effects, and in the
region ahead of the front the depolarisation effect overbalances the
hyperpolarisation, and the front jumps forwards. The later evolution
depends on how far the wavefront jumped. If the stimulus was above the
threshold (see Fig. 10, upper row), the front advances to
the region where the tissue has not recovered yet, and the antegrade
propagation is not possible. Hence, the front retracts, i.e. begins to
collapse backwards, and the excited region shrinks until it vanishes,
as the depolarising wavefront moves backwards and the repolarisation
waveback carries on moving forwards.
Figure 10:
Snapshots from movies of suprathreshold (above, with 
)
and subthreshold (below, with 
) defibrillation by a
spatially uniform depolarising current pulse 
of a spiral wave
shown on fig. 3. Time moments are chosen 0, 3, 40
and 
(left to right) measured since the beginning of the
stimulus.
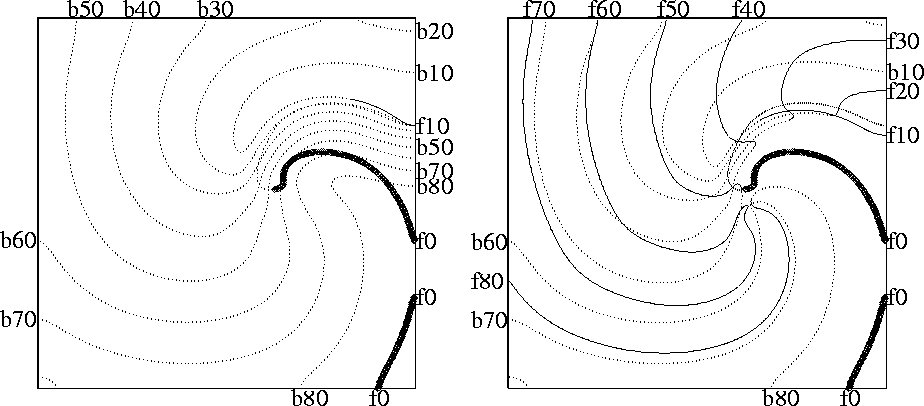
Figure 11:
Wavefronts (solid lines) and wavebacks (dotted lines) visualised as
isolines every 
during (left) the suprathreshold and
(right) subthreshold defibrillating shocks of
Fig. 10. The first isoline (front shown by bold
line) is just before the defibrillating pulse was applied; the spiral
wave is rotating counterclockwise. Labels code the isolines'
type (letters b/f) and time in 
since the shock application.
A smaller (subthreshold) shock will produce a smaller advance in the position of the front and thus allow the possibility for it to recover its forward propagation. This possibility depends on two factors, the refractory state of the medium and the front curvature, which in turn depends on the geometry of the wavefront at the moment of the shock delivery. The lower row of Fig. 10 shows the case when, after the shock, the propagation resumes not along the whole front, but only at the most concave segment of it, where the front curvature assist the propagation. This is sufficient to resume the rotation of the spiral wave. So, from this example it can be seen that DFT measured in two dimensions should be usually higher than that in one dimension.
We have applied the theory of [35] and [36]
to calculate the one-dimensional DFT based on the properties of the
single cell version of equations (4) and the restitution
curve of original 1D model; this was found to be about 
. The
numerically computed 1D DFT was approx. 
, and in 2D, approx.
. These values are for the rectangular current pulses of
duration, and with the intracellular conductance assumed
, which is, e.g., the conductance of a 
cube of
myoplasm with specific resistivity of 
.
(note that only the ratio of 
is
used in the model).
Assuming the orders of magnitude for
cell length 
,
cell cross-section 
and heart cross-section 
,
the value of of 
corresponds
to the electric field
and the transcardiac current
which quite agrees
with the experimental DFT 
for electric field
[39] and 
for transcardiac current
[40]; as we mentioned above, the theory allows absolute
comparison with experiment only in the order of magnitude.
The close coincidence of 1D and 2D estimations of DFT shows that the
2D effects are less important than other simplifications used. We
believe that the crudest of the simplifications of that theory,
after assumptions of uniformity of external current and tissue
properties, is the use of the Fife technique [41], considering the
excitation wave propagation as trigger waves in bistable media with one
fast variable (the transmembrane voltage), while the conditions of
propagation are governed by slow and local evolutions. The evolution in
the OGPV model is more complicated, as there are three other
variables 
of characteristic time scales roughly comparable to
that of the transmembrane voltage.
