We now apply this approach to evaluate the defibrillation threshold for a tissue, i.e. the amplitude of an externally applied current pulse necessary to abolish all propagating waves, and compare it with the prediction of the asymptotic theory of defibrillation for our model. The theory was described by Pumir & Krinsky [1996] and is based on separate consideration of the slow and fast processes during the process of propagation [Fife, 1976, Tyson & Keener, 1988]. During re-entrant activity and fibrillation, propagation in the whole heart is an irregular and changing pattern of waves and wavelets [Gray & Jalife, 1996]. The asymptotic theory of defibrillation assumes that on the fast time scale the medium has two alternative stable equilibria, which depend on the slow variables. The propagation of the wavefront, in the fast time scale, is a trigger wave between the equilibria that is either ``antegrade'', when the excited region grows, or ``retrograde'' propagation, when the excited region shrinks. The wavefront of a propagating pulse is an antegrade trigger wave, and its back a retrograde wave. In a resting medium, the upper, ``excited'' equilibrium is more stable, so a suprathreshold perturbation produces an antegrade trigger wave, and the excited region expands. During the excited state, the evolution of the slow variables lowers the stability of the excited state while the stability of the resting state increases, until a retrograde trigger wave can propagate.
Figure 3:
(a) Subthreshold (600 nA, 2 ms) and (b) suprathreshold
(800 nA, 2 ms) response of a re-entrant wave in
one-dimensional ring to a defibrillating shock. In both cases the
wavefront is initially advanced, in the suprathreshold case the
wavefront collapses back to its position at the time the pulse was
applied, and meets its waveback. The circumference of the ring is
60 mm, and the membrane potential is displayed every 2 ms,
i.e. the conduction velocity of the wave before defibrillation
was 300 mm/s.
In this approximation a wavefront cannot spontaneously change direction of propagation. When a defibrillating shock is applied to the whole medium, if the intensity of the shock is high enough, then all the cells of the medium can be thrown into the excited state, and thereafter only retrograde waves will occur throughout the medium and these will trigger all the medium into the resting state. Driving all the medium into the excited state provides a simple understanding of defibrillation. However it is not necessarily exact. First, not all the cells may be excitable, i.e. have the alternative ``upper equilibrium'' at the moment of shock delivery. Second, the requirement of all the excitable cells to be triggered into the excited state is excessive. Defibrillation requires that only retrograde waves are generated after it. To ensure this, it is only necessary to excite all those cells which have the resting state as the more stable state, and it is not necessary to excite those which have the excited state as the more stable.
The boundary between these classes of cells is in the state space of the slow variables, and corresponds to the values of these variables when the two equilibria are equally stable. If u is much faster than both v and w, this ``equal stability'' is represented by a ``Maxwell rule'', for the right-hand side of the fast excitability equation:
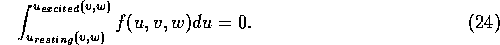
When there is only one slow variable w, as in the FitzHugh-Nagumo
system considered by Pumir & Krinsky [1996], this equality has a
unique solution at the ``critical value''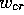 
, and the
defibrillation condition is then reduced to the requirement, that all
cells with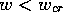 
should be excited. However,the ``Maxwell point''
falls exactly at the centre of symmetry of the excitability model used
by Pumir & Krinsky [1996], f(u,v,w)=F(u)-w with a cubic F, and
for this model, in the style of (14), a cell at the
critical point cannot be excited by a uniform field of any magnitude.
Figure 4:
Velocities of forward fronts of excitation waves, mm/s, as functions of
interwave intervals, ms.
In biophysical excitation equations there is no such symmetry and so
the theory is applicable as long as the realistic ``slow processes''
v and w are slow enough for the asymptotic approach to be valid.
The margin (24) between preferably-excited and
preferably-resting cells is a manifold of codimension 1, and so finding
the exact defibrillation condition would imply finding the points with
the highest threshold on this manifold. We do not need to search the
whole space, only in a subset, corresponding to states of cells present
in the tissue in the moment of defibrillation. Estimation of the
defibrillation threshold requires a model of fibrillation, as well as a
model for the defibrillation process. We estimated the velocities of
propagation of wavefronts of excitation pulses driven at the highest
possible frequencies,
provided by a spiral wave solution. Since, as it was mentioned in
Section 7, the excitation properties are strongly
influenced by the pre-history of excitations, we used here exactly the
same pre-conditioning procedure as for Fig. 2. The dependence
of premature pulse propagation velocity on the coupling interval is
shown in Fig. 4. A 1.5 mm long one-dimensional model governed by
(23) without external current was integrated with boundary
conditions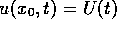 
at one end, and non-flux condition on the
other, where U(t) was the transmembrane voltage profile of a
developing spiral wave solution recorded at a point far from the core
(see Fig. 2(b) in [Biktashev & Holden 1996], point `D').
Thus, pulses propagated through the fibre in the same sequence as they
typically do in 2D during development of a spiral wave. After 14 such
pulses, the 15th one was initiated prematurely with a controlled
advance in time, and its velocity was measured via crossing times at
points distant 0.5 and 1.0 mm from the boundary. The smallest coupling
interval we could obtain was 97 ms. Comparison with the
threshold-interval plot (Fig. 2), gives the excitation threshold
corresponding to this interval of 840 nA,
and this provides the estimate of the defibrillation threshold. This
theoretical estimate has been obtained from the threshold-interval
relation for the ODE models including the models of external action
(15), (19) and (22), and from the
velocity-period relation for one-dimensional experiments without any
external action, connected by the asymptotic theory of defibrillation.
An independent ``direct'' estimation of this threshold was made in
experiments with model (23), which is both spatially
extended and involves external stimulation. For a one-dimensional fibre
with periodic boundary conditions a uniform external field can
extinguish a recirculating wave; the stimulus pulse forces the
wavefront forward, and the wavefront then decays back to its position
at the time of stimulation, while waveback continues to propagate
(Fig. 3). All activity is extinguished when the waveback meets
the wavefront. The resulting defibrillation threshold for these
computations is 740 nA, which is similar to the ``theoretical''
estimation of 840 nA.
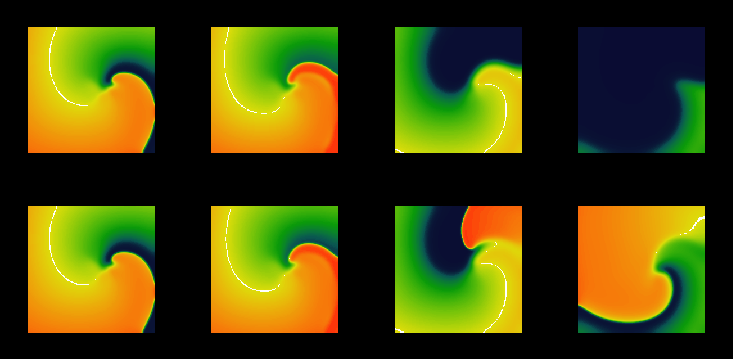
Figure 5:
Snapshots from movies of suprathreshold (above, with 800 nA/cell)
and subthreshold (below, with 650 nA/cell) defibrillation by a
spatially uniform 2 ms depolarising current pulse of a spiral wave
in a model of a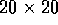 
mm slice of
ventricular tisue, with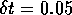 
ms and 
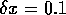mm, and cellular excitability described by the
Oxsoft guinea pig ventricular model [Noble 1990, Biktashev & Holden 1996].
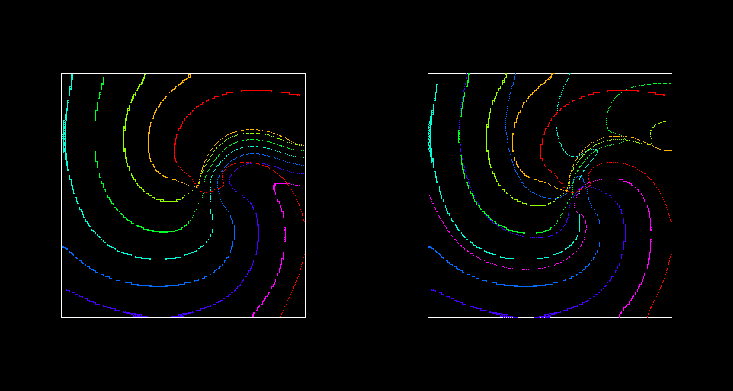
Figure 6:
Wavefronts and wavebacks visualised as -10 mV isolines every 10 ms during (left) the
suprathreshold and (right) subthreshold defibrillating shocks of
Fig. 5. The red isoline is just before the defibrillating
pulse was applied; the spiral wave is rotating counterclockwise.
For a spiral wave solution of the two-dimensional analogue of
(23), there is a narrow gap between between waveback of the
spiral wave and the following wavefront. The response of such a
counter-clockwise rotating re-entrant spiral (Fig. 5,
6) to a brief defibrillating pulse is similar to that seen
in the one-dimensional model: the wavefront is forced forward, and then
relaxes back to its position at the time the shock was applied, while
the waveback continues to rotate counter-clockwise. All activity is
extinguished when the waveback reaches the wavefront. The effect of
the defibrillating pulse is mainly determined by the behaviour of the
wavefront just after its application: if it was strong enough to make
the front jump ahead into a region of refractory medium where it cannot
propagate but instead retracts, then it continues to retract and so the
defibrillation is successful as all activity is extinguished. The
predominance of the effect on the wavefront follows naturally from the
fact that the wavefront is determined by the fast processes, with a
time constant 
close to the duration of the defibrillating
shock. In this particular model, the defibrillation threshold was
found to be 750 nA.
Since the external currents occurring in our calculations are in nA per cell, we cannot directly compare these results with clinical or experimental data. However, the dimensionless ratio between the excitation and defibrillation thresholds can be compared. In our model, this ratio has been found to be about 1.5.
Real cardiac tissue is heterogeneous and so the experimental estimation of the excitation threshold gives the threshold for the most excitable tissue, while the experimental estimation of the defibrillation threshold gives the threshold for elimination of the activity in all the tissue. Thus the exprimental ratio will always be more than this theoretical value, -- e.g., the ratio mentioned by Dillon [1991] is about 10.
